許多應用都要求能夠在頻域內開展工作。本文將介紹如何處理FPGA設計中的頻域問題。
對許多工程師而言,在頻域中開展工作不如在時域中開展工作那么自然,可能是因為頻率與復雜的數學運算有關。但是要充分發揮賽靈思FPGA解決方案的潛力,您需要在這兩個域中自由切換。
令人欣慰的是詳細地掌握頻域并不像您最初想象的那樣令人生畏。不管是您自己設計的定制模塊還是市場上現有的IP模塊,都能幫助您輕松轉入轉出頻域。同時在頻域中實現高速處理的方法也不乏其數。
時域還是頻域?
工程師既能在時域中檢驗和處理信號,根據時間分析信號,也能在頻域中檢驗和處理信號,根據頻率分析信號。項目對工程師的主要要求之一,就是應該知道什么時候應該開展哪種分析。
一般在電子系統中,需要考查的信號是一個不斷變化的電壓、電流或頻率。它可以是傳感器的輸出,也可能是系統其他部分生成的輸出。在時域中,您可以測量信號的幅度、頻率和周期,以及信號上升或下降時間等更有意義的參數。實驗室環境中觀察時域信號常用的是示波器或邏輯分析儀。
但是信號的一些參數體現在頻域內。必須在頻率中分析這些參數,才能解讀其中包含的信息。在頻域中可以識別信號的頻率分量、各自的幅度和每種頻率的相位。由于在頻域中便于開展卷積運算,因此在頻域中工作也能大大簡化信號處理。卷積是一種將兩種信號混合成第三種信號的數學方法。和時域分析一樣,如果想要在實驗室環境中觀察頻域信號,可以使用頻譜分析儀。
根據信號的類型,如重復性還是非重復性、離散還是非離散,有多種方法可用于時域和頻域之間的變換
對某些應用而言在時域中工作比較合適,例如用于監測更大型系統的電壓或溫度的系統。雖然噪聲可能是個問題,在許多情況下取一定數量樣本的平均值就可以滿足要求。但對其他應用來說,最好是在頻域中開展工作。例如需要從另一信號中過濾某種信號的信號處理應用,或是需要將信號與噪聲源分離的信號處理應用,最好在頻率中開展分析。
由于采樣是在時域中完成的,在時域中工作基本不需要對量化數字信號進行后處理。與此相反,在頻域中開展工作首先要求應用將量化數據從時域變換到頻域。同樣,從頻域輸出后處理過的數據時,需要從頻率轉回到時域。
如何進行變換?
根據信號的類型,如重復性還是非重復性、離散還是非離散,有多種方法可用于時域和頻域之間的變換,包括傅里葉級數、傅里葉變換和Z變換。尤其是在電子信號處理和FPGA應用中,最常用到的變換是離散傅里葉變換(DFT),傅里葉變換中的一種。工程師使用DFT分析具有周期性和離散性的信號,即由一定數量均勻分布在采樣頻率中的n位樣本組成的信號。在許多應用中這種信號一般來自系統內的ADC。
簡單地說,DFT的工作原理就是把輸入信號分解成代表信號正弦分量和余弦分量的兩個輸出信號。因此對由N個樣本組成的時域序列,DFT會返回兩組N/2+1個余弦波樣本和正弦波樣本,分別被稱為實分量和虛分量(圖1)。實樣本和虛樣本的寬度為n位輸入信號寬度的n/2。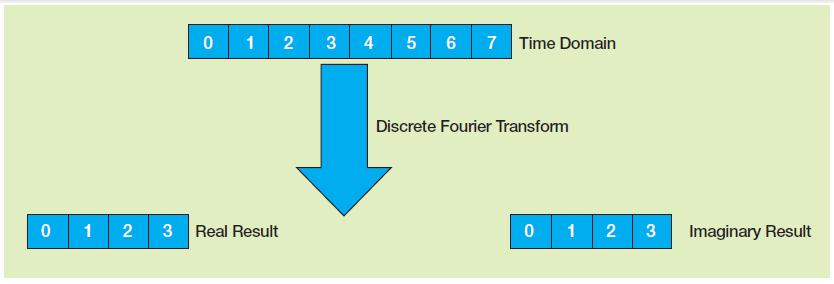
圖1 - 時域中的n位被變換為頻域中n/2實位和n/2虛位
計算DFT的算法十分簡明,如下式所示:
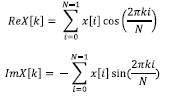
其中,x[i]代表時域信號;i的取值為0到N-1;k的取值為0到N/2。這種方法被稱為關聯法,其功能是將輸入信號與對應迭代的正弦波或余弦波相乘,以確定其幅度。
當然,您可能想要在應用中的某點從頻域變換回時域。為此可以使用綜合公式,它將實波形和虛波形結合起來,重建時域信號,即:
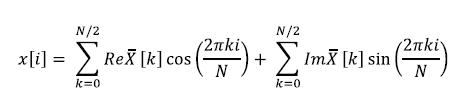
但ReX和ImX是正弦波和余弦波的縮放結果,因此需要進行縮放。除Rex[0]和Rex[N/2]之外的所有情況,ReX和ImX的值均為ReX[k]或ImX[k]除以N/2。對Rex[0]和Rex[N/2],則除以N。出于明顯的理由,這種運算被稱為傅里葉反變換(IDFT)。
通過探討確定DFT和IDFT所使用的算法,可能有助于了解如何加以利用這些算法。
您可以使用Octave、MATLAB®乃至Excel對所采集的數據進行DFT計算。許多實驗室工具,如示波器,也能根據需要執行DFT計算。
不過需要指出的是上述的DFT和IDFT被稱為實DFT和實IDFT,因為輸入的是實數而非復數。很快就會清楚為何要了解這一點。
需要進行變換的地方
從電信到圖像處理、雷達和聲納,難以想象有比傅里葉變換更強大、更適合并可實現FPGA中的分析技術。實際上DFT是最常用FPGA應用之一(即,生產有限輸入響應(FIR)濾波器系數)的基礎(參閱賽靈思中國通訊第43期《數字濾波器設計與實現詳情》)。
但其用途不局限于濾波。DFT和IDFT還可用于電信處理中,用于執行電信通道的信道化和重組。在頻譜監測應用中,它們可用來判斷監測帶寬內的頻率構成。在圖像處理中,它們用于處理圖像卷積,供濾波器內核開展圖像模式識別等操作。所有這些應用在實現過程中一般使用比上文介紹的更有效的算法來計算DFT。
總而言之,了解DFT并將其實現在FPGA中是每個FPGA開發人員的必備技能。
基于FPGA的實現方式
上文介紹的DFT和IDFT的實現一般采用嵌套循環,每個循環完成N次計算。因此實現DFT計算所需的時間為:
DFTtime = N * N * Kd ft
其中,Kdft表示完成每次迭代的處理時間。顯然這種方法實現起來極為耗時。為此FPGA中實現DFT一般使用快速傅里葉變換算法(FFT)。FFT常常被稱為我們時代最重要的算法,因為它對許多行業都產生根本性的影響。
FFT與DFT算法稍有不同,它計算的是復數DFT,即它需要實時域信號和虛時域信號,得到的結果的寬度是n位而非n/2位。這意味著如果需要計算實DFT,必須首先把虛部設為0,然后把時域信號轉移到實部。如果要在賽靈思FPGA實現FFT,可以有兩種選擇。您可以使用您選擇的HDL重新編寫FFT,也可以使用Vivado®設計套件IP Catalog或其他來源提供的FFT IP。除非有不得已的原因不能使用IP,為縮短開發時間,一般都應該選擇IP。
FFT的基本方法是將時域信號分解為一系列單點時域信號。因為樣本被重新排序,這個過程常被稱為位反轉。如果沒有位反轉算法這一捷徑可走,那么創建單點時域信號的級數可以用Log2 N計算得到,其中,N表示位數。
隨后使用這些單點時域信號計算每個點的頻譜。這一計算相當簡單,因為頻譜與單點的時域相等。
這些單頻點的重組是FFT算法最復雜環節。必須每一級重組一次這些頻點,恰好是時域分解的反向操作。因此要重建頻譜需要Log2 N級,這里就是著名的蝶形FFT發揮作用的地方。
與DFT的執行時間相比,FFT用時為:
FFTtime = K f ft * N Log2 N
與計算DFT相比,執行時間明顯縮短。
在FPGA中實現FFT算法時,還必須考慮FFT采樣數。FFT采樣數將決定本底噪聲,在此之下將無法再看到有用信號。FFT采樣數還將決定頻點之間的間距。使用下面的公式可以確定FFT采樣數:
其中,n為時域中量化位的數量,FFTSize為FFT采樣數。對基于FPGA的設計,這一般是2的冪,如256、512、1,024等。頻點可采用下列公式計算出其等間隔:
舉個非常簡單的例子,在采樣頻率(FS)為100 MHz的情況下,使用128個FFT樣本可實現0.39 Hz的頻率精度。這意味著如果頻率彼此之間的間隔小于0.39 Hz將無法分辨。
高速采樣
許多FPGA中的FFT應用和較高性能的系統都工作在非常高的頻率下。高頻運行會產生自己特有的設計難題。
因為在高頻下無法維持奈奎斯特采樣率(每個周期兩個樣本),因此需要不同的方法。例如使用2.5 GHz采樣率采樣3 GHz全功率帶寬模擬輸入。運用奈奎斯特頻率法則,高于1.25 GHz的信號將被混疊到有用的第一個奈奎斯特域中。這些混疊鏡像將成為基本信號的諧波分量,因此包含與非混疊信號相同的信息,如圖2所示。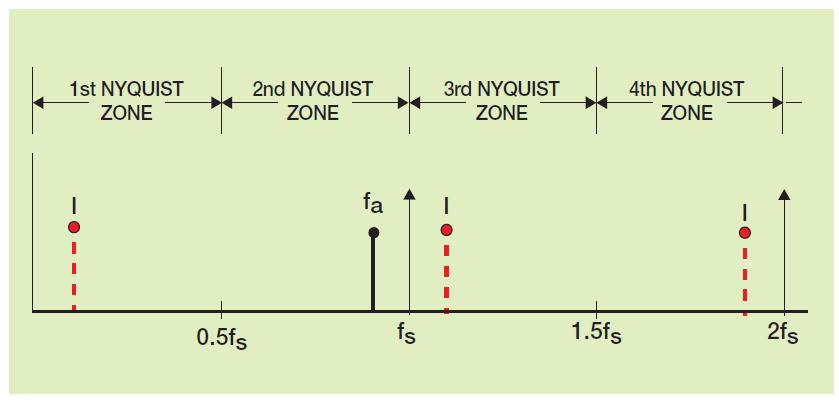
圖2 - 奈奎斯特域與混疊
要判斷得到的諧波或諧波成分的頻率布局,可使用下列算法:
Fharm = N × Ffund
IF (Fharm = Odd Nyquist Zone)
Floc = Fharm Mod Ffund
Else
Floc = Ffund-(Fharm Mod Ffund)
End
其中,N表示有用諧波的整數。
繼續前述例子,如果采樣率為2,500 MHz,基頻為1,807 MHz,則會在第一奈奎斯特域中產生693 MHz的諧波成分,供在FFT中進一步處理。
在掌握了頻譜的基本知識之后,下一個需要考慮的關鍵因素是如何將這些ADC和DAC器件與FPGA連接在一起。在上面所述的實例中,,無法從ADC接收頻率為采樣頻率一半(采樣率為2.5 Gbps)的數據。為此,高性能數據轉換器使用多路復用的數字輸入輸出,該輸入輸出工作在較低頻率下,一般為轉換器的采樣頻率的四分之一或二分之一(即FS/4或 FS/2)。
FPGA通過多個數據流接收到數據后,如果希望執行DFT,那么下一個要解決的問題就是如何在FPGA內處理數據。包括電信和射電天文在內的多種應用常用的方法是使用重組或分解FFT結構(如圖3所示)。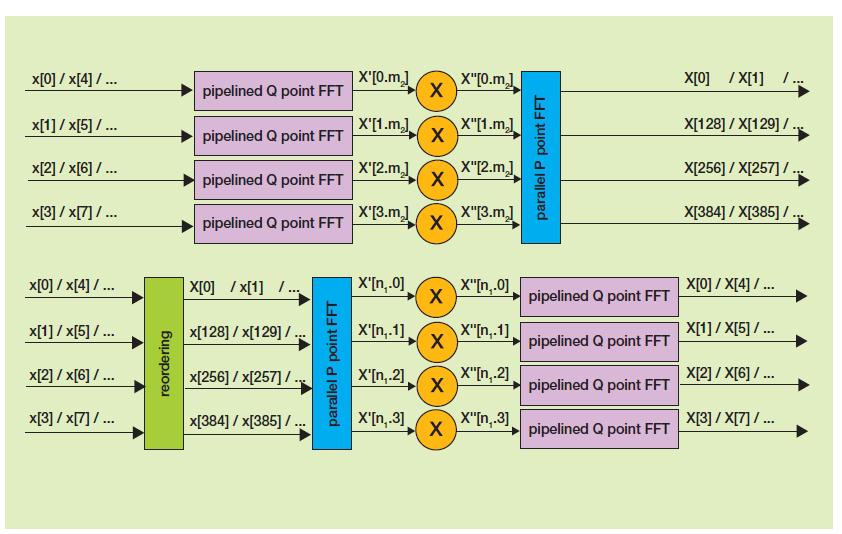
圖3 - 分解與重組FFT結構
雖然這種應用與直接FFT相比更復雜,使用這種方法能夠實現高速處理。
正您所見,在頻域中工作并非像最初想象的那樣困難,特別是有IP模塊幫助轉入轉出頻域的情況下。此外還有多種方法可供選擇,幫助您實現高速處理。
EP2S130F1020I4N
EP3SL340F1517I4
EP3SL340F1517C3N
EP1S40F1508I6
EP1S40F1508I6N
EP1S40F1508C6N
EP2S180F1020C4
EP2S180F1020I5
EP2S180F1020I4
EP2S180F1020C3
EP2S180F1020I5N
EP2S180F1508C4N
EP2S180F1020C4N
EP2S180F1020I3N
EP2S180F1020C5N









