HLMP-6300-F0021 相位差
發布時間:2019/10/4 23:41:51 訪問次數:1271
HLMP-6300-F0021如果將一個正弦電壓加到一個電阻上,那么流過電阻上的電流也是正弦波。因為歐姆定律指出電流與電壓成正比c圖3.1-8在同一時間軸上畫出了電流和電壓的波形。注意:電壓正向增加,電流隨之正向增加;電壓反向增加,電流也隨之反向增加。在所有時間內,電壓和電流波形同步變化,因此稱這兩個波形同相。
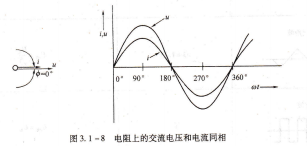
圖3,1-8 電阻上的交流電壓和電流同相
圖3.1-9畫出了兩個相位不同的電壓波形。在起始點0°,“1到達正峰值,電壓L2為零。由于這兩個波形不是在同一時刻到達最大值和最小值,因此稱這兩個波形之間存在相位差c該圖中兩個波形之間的相位差為90°。
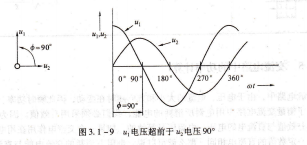
圖3,1-9 仍I電壓超前于揚2電壓90°
為了更進一步地描述兩個波形之間的相位關系,引人了超前和滯后兩個名詞。一個波形超前或滯后于另一個波形的大小用角度來衡量。對于圖3.1-9所示的兩個波形來說,可以這樣描述:“2電壓滯后于L1電壓90°或“j電壓超前干I‘2電壓90°。相位差一般用Δφ表示,Δφ=φ1-φ2。其中φ1表示・1的初相位,φ2表示“2的初相位。因此,我們可以對Δφ的數值加以討論:
相位差的取值范圍為:0°(Δφ<180°。
當Δφ>0°時,ul電壓超前于“2電壓;
當Δφ(0°時,IJ 1電壓滯后于△2電壓;
當Δφ=0°時,乙l電壓與己2電壓同相;
當Δφ=90°時,%電壓與乙2電壓正交;如圖3.1-9所示。
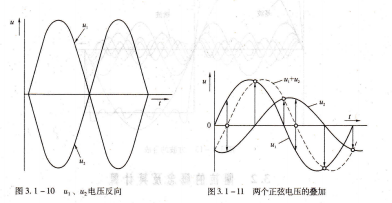
當Δφ=180°時,“1電壓與乙2電壓反向;如圖3.1-10所示。
在電子電路中,“正交”和“反相”兩種情況是應用最多的。在后續教材中我們會在具體的電路中加以詳細的描述。應當注意,研究兩個正弦波的相位差,一般是指兩個頻率相同的正弦波。因為這樣的兩個正弦波之間的相位差總是常數。而頻率不同的兩個正弦波之間的相位差不再是一個常數,它是隨時間變化的。因此,研究其相位差的意義不大。
正弦交流電的疊加,當兩個或兩個以上的正弦波電壓加到同一個電路中時,它們之間會產生疊加。其疊加結果與正弦波的頻率有關。
兩個頻率相同的正弦電壓相疊加,其波形如圖3.1-11所示,從圖中可以看到,疊加后
的波形仍然是同頻率的正弦波,但其幅度和初相位將發生變化。如果將兩個同頻率的正弦波相乘,則可以得到一個兩倍頻率的正弦波,如圖3.1-12所示。此外,在曲線上還可以看出正弦波形的斜率變化率,該變化率也是一條正弦曲線。
HLMP-6300-F0021如果將一個正弦電壓加到一個電阻上,那么流過電阻上的電流也是正弦波。因為歐姆定律指出電流與電壓成正比c圖3.1-8在同一時間軸上畫出了電流和電壓的波形。注意:電壓正向增加,電流隨之正向增加;電壓反向增加,電流也隨之反向增加。在所有時間內,電壓和電流波形同步變化,因此稱這兩個波形同相。

圖3,1-8 電阻上的交流電壓和電流同相
圖3.1-9畫出了兩個相位不同的電壓波形。在起始點0°,“1到達正峰值,電壓L2為零。由于這兩個波形不是在同一時刻到達最大值和最小值,因此稱這兩個波形之間存在相位差c該圖中兩個波形之間的相位差為90°。

圖3,1-9 仍I電壓超前于揚2電壓90°
為了更進一步地描述兩個波形之間的相位關系,引人了超前和滯后兩個名詞。一個波形超前或滯后于另一個波形的大小用角度來衡量。對于圖3.1-9所示的兩個波形來說,可以這樣描述:“2電壓滯后于L1電壓90°或“j電壓超前干I‘2電壓90°。相位差一般用Δφ表示,Δφ=φ1-φ2。其中φ1表示・1的初相位,φ2表示“2的初相位。因此,我們可以對Δφ的數值加以討論:
相位差的取值范圍為:0°(Δφ<180°。
當Δφ>0°時,ul電壓超前于“2電壓;
當Δφ(0°時,IJ 1電壓滯后于△2電壓;
當Δφ=0°時,乙l電壓與己2電壓同相;
當Δφ=90°時,%電壓與乙2電壓正交;如圖3.1-9所示。
當Δφ=180°時,“1電壓與乙2電壓反向;如圖3.1-10所示。
在電子電路中,“正交”和“反相”兩種情況是應用最多的。在后續教材中我們會在具體的電路中加以詳細的描述。應當注意,研究兩個正弦波的相位差,一般是指兩個頻率相同的正弦波。因為這樣的兩個正弦波之間的相位差總是常數。而頻率不同的兩個正弦波之間的相位差不再是一個常數,它是隨時間變化的。因此,研究其相位差的意義不大。
正弦交流電的疊加,當兩個或兩個以上的正弦波電壓加到同一個電路中時,它們之間會產生疊加。其疊加結果與正弦波的頻率有關。
兩個頻率相同的正弦電壓相疊加,其波形如圖3.1-11所示,從圖中可以看到,疊加后
的波形仍然是同頻率的正弦波,但其幅度和初相位將發生變化。如果將兩個同頻率的正弦波相乘,則可以得到一個兩倍頻率的正弦波,如圖3.1-12所示。此外,在曲線上還可以看出正弦波形的斜率變化率,該變化率也是一條正弦曲線。




 公網安備44030402000607
公網安備44030402000607





