GS-29-622二極管的極間電容
發布時間:2019/10/31 20:37:31 訪問次數:3138
GS-29-622在二極管電路中,其他條件不變,溫度升高時,二極管的電流將會產生怎樣的變化趨勢?硅二極管和鍺二極管哪種受溫度影響更大?
二極管的極間電容主要影響它的什么工作特性?
在電子技術中,二極管電路得到廣泛的應用。本節重點介紹采用簡化模型,分析幾種基本的二極管電路,如限幅電路、開關電路、低電壓穩壓電路等。
簡單二極管電路的圖解分析方法.二極管是一種非線性器件,因而其電路一般要采用非線性電路的分析方法,相對來說比較復雜,而圖解分析法則較簡單,但前提條件是已知二極管的y-r特性曲線。下面通過一個例子加以說明。
二極管電路如圖3.4.1a所示,設二極管的V-r特性曲線如圖b所示。已知電源yDD和電阻R,求二極管兩端電壓vD和流過二極管的電流jD。

二極管電路(a)電路圖 (b)圖解分析二極管V-J特性曲線率為T責的負載線
解:由電路的KVL方程,可得在id=vdd-uo/r (3.4.1)
可寫成id=-1/rud+1/rvdd (3.4.2)
二極管的基本咆蹯及其分析方法,該式在圖b的坐標系中是一條斜率為-1/R釣直線,稱為負載線。在圖中做出該負載線,其與二極管y~J特性曲線交點Q的坐標值(yD,fD)即為所求。Q點稱為電路的工作點。
用圖解法求解二極管電路比較簡單直觀,但前提條件是已知二極管的y~f特性曲線,而在二極管實際應用電路中,這個要求往往是不現實的。所以,圖解法并不實用,但對理解電路的工作原理和相關重要概念卻有很大幫助。
為閱讀方便,將二極管的/-J特性關系式(3.2.3)重寫如下(此處原式中的n取1):
iD=is(euD/vT-1) (3.4.3)
通過聯立求解式(3.4.1)和(3.4.3),便可求出vD和iD。顯然,求解的是指數方程。這種方法稱為迭代法,解方程的過程比較復雜。特別是電路復雜后,迭代法將變得非常復雜。
實際上,式(3.4.3)是二極管y~f特性一個很好的模型,稱之為指數模型。利用它并根據數學迭代原理,可以較準確地分析二極管電路,但一般要借助計算機來完成(如sPICE程序等)。
以上分析看出,無論是圖解法還是迭代法都不實用。工程上,通常在一定條件下,利用簡化模型代替二極管非線性特性,來分析二極管電路,從而使分析大為簡化。簡化模型分析方法是非常簡單有效的工程近似分析方法。
二極管電路的簡化模型分析方法,二極管v~l特性的建模,理想模型,圖3.4.2a表示理想二極管的/-J特性,其中的虛線表示實際二極管的y-J特性。圖3.4.2b為理想二極管的代表符號。由圖a可見,在正向偏置時,其管壓降為0Ⅴ,而當二極管處于反向偏置時,認為它的電阻為無窮大,電流為零。在實際的電路中,當電源電壓遠比二極管的管壓降大時,利用此模型來近似分析是可行的。
恒壓降模型,這個模型如圖3.4.3所示,其基本思想是當二極管導通后,其管壓降認為是恒定的,且不隨電流而變,典型值為0.7Ⅴ(硅管)。不過,這只是當二極管
的電流jD近似等于或大于1mA時才是正確的。該模型提供了合理的近似,因此應用也較廣。
折線模型,為了較真實地描述二極管y~f特性,在恒壓降模型的基礎上,作一定的
二極管及其基本電路,理想模型,(a)y-J特性 (b)代表符號 (c)正向偏置時唧電路模型(d)反向偏置時的電路模型修正,即認為二極管的管壓降不是恒定的,而是隨著通過二極管電流的增加而增加,所以在模型中用一個電池和一個電阻rD來作進一步的近似(如圖3.4.4)。這個電池的電莊選定為二極管的門坎電壓⒕h,約為0.5Ⅴ(硅管)。

至于rD的值,可以這樣來確定,即當二極管的導通電流為1mA時,管壓降為o.7Ⅴ,于是rD的值可計算如下:0,7V-0.5Ⅴ恒壓降模型(a)y-f特性 (b)電路模型,由于二極管特性的分散性,1mAah和rD的值不是固定不變的。

二極管的基本電蹯及其分析方法,小信號模型在圖3.4.1中串聯一個交流信號源vs,得到圖3.4.5a的電路。當vs=0時,電路中只有直流量,二極管兩端電壓和流過二極管的電流就是圖3,4.1b中0點的值。為方便說明,將圖重畫于圖3.4.5b中。此時,電路處于直流工作狀態,也稱靜態,0點也稱為靜態工作點。當vs=ymsin ωt時(v<<yD),電路的負載線為
rd=-0.7v-0.5v/1ma=200
根據vθ的正負峰值+‰和-‰圖解可知,工作點將在o′和o″之間移動,則二極管電壓和電流變化為ΔvD和ΔjD。
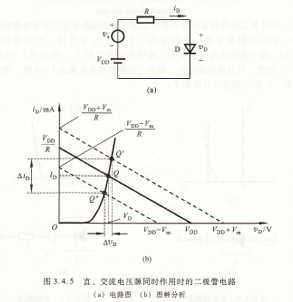
直、交流電壓源同時作用時的二極管電路(a)電路圖 (b〉圖解分析
由上看出,在交流小信號vs的作用下,工作點沿v-r特性曲線,在靜態工作點o附近小范圍內變化,此時可把二極管v-f特性近似為以0點為切點的一條直線,其斜率的倒數就是小信號模型的微變電阻rd,由此得到小信號模型。
GS-29-622在二極管電路中,其他條件不變,溫度升高時,二極管的電流將會產生怎樣的變化趨勢?硅二極管和鍺二極管哪種受溫度影響更大?
二極管的極間電容主要影響它的什么工作特性?
在電子技術中,二極管電路得到廣泛的應用。本節重點介紹采用簡化模型,分析幾種基本的二極管電路,如限幅電路、開關電路、低電壓穩壓電路等。
簡單二極管電路的圖解分析方法.二極管是一種非線性器件,因而其電路一般要采用非線性電路的分析方法,相對來說比較復雜,而圖解分析法則較簡單,但前提條件是已知二極管的y-r特性曲線。下面通過一個例子加以說明。
二極管電路如圖3.4.1a所示,設二極管的V-r特性曲線如圖b所示。已知電源yDD和電阻R,求二極管兩端電壓vD和流過二極管的電流jD。

二極管電路(a)電路圖 (b)圖解分析二極管V-J特性曲線率為T責的負載線
解:由電路的KVL方程,可得在id=vdd-uo/r (3.4.1)
可寫成id=-1/rud+1/rvdd (3.4.2)
二極管的基本咆蹯及其分析方法,該式在圖b的坐標系中是一條斜率為-1/R釣直線,稱為負載線。在圖中做出該負載線,其與二極管y~J特性曲線交點Q的坐標值(yD,fD)即為所求。Q點稱為電路的工作點。
用圖解法求解二極管電路比較簡單直觀,但前提條件是已知二極管的y~f特性曲線,而在二極管實際應用電路中,這個要求往往是不現實的。所以,圖解法并不實用,但對理解電路的工作原理和相關重要概念卻有很大幫助。
為閱讀方便,將二極管的/-J特性關系式(3.2.3)重寫如下(此處原式中的n取1):
iD=is(euD/vT-1) (3.4.3)
通過聯立求解式(3.4.1)和(3.4.3),便可求出vD和iD。顯然,求解的是指數方程。這種方法稱為迭代法,解方程的過程比較復雜。特別是電路復雜后,迭代法將變得非常復雜。
實際上,式(3.4.3)是二極管y~f特性一個很好的模型,稱之為指數模型。利用它并根據數學迭代原理,可以較準確地分析二極管電路,但一般要借助計算機來完成(如sPICE程序等)。
以上分析看出,無論是圖解法還是迭代法都不實用。工程上,通常在一定條件下,利用簡化模型代替二極管非線性特性,來分析二極管電路,從而使分析大為簡化。簡化模型分析方法是非常簡單有效的工程近似分析方法。
二極管電路的簡化模型分析方法,二極管v~l特性的建模,理想模型,圖3.4.2a表示理想二極管的/-J特性,其中的虛線表示實際二極管的y-J特性。圖3.4.2b為理想二極管的代表符號。由圖a可見,在正向偏置時,其管壓降為0Ⅴ,而當二極管處于反向偏置時,認為它的電阻為無窮大,電流為零。在實際的電路中,當電源電壓遠比二極管的管壓降大時,利用此模型來近似分析是可行的。
恒壓降模型,這個模型如圖3.4.3所示,其基本思想是當二極管導通后,其管壓降認為是恒定的,且不隨電流而變,典型值為0.7Ⅴ(硅管)。不過,這只是當二極管
的電流jD近似等于或大于1mA時才是正確的。該模型提供了合理的近似,因此應用也較廣。
折線模型,為了較真實地描述二極管y~f特性,在恒壓降模型的基礎上,作一定的
二極管及其基本電路,理想模型,(a)y-J特性 (b)代表符號 (c)正向偏置時唧電路模型(d)反向偏置時的電路模型修正,即認為二極管的管壓降不是恒定的,而是隨著通過二極管電流的增加而增加,所以在模型中用一個電池和一個電阻rD來作進一步的近似(如圖3.4.4)。這個電池的電莊選定為二極管的門坎電壓⒕h,約為0.5Ⅴ(硅管)。

至于rD的值,可以這樣來確定,即當二極管的導通電流為1mA時,管壓降為o.7Ⅴ,于是rD的值可計算如下:0,7V-0.5Ⅴ恒壓降模型(a)y-f特性 (b)電路模型,由于二極管特性的分散性,1mAah和rD的值不是固定不變的。

二極管的基本電蹯及其分析方法,小信號模型在圖3.4.1中串聯一個交流信號源vs,得到圖3.4.5a的電路。當vs=0時,電路中只有直流量,二極管兩端電壓和流過二極管的電流就是圖3,4.1b中0點的值。為方便說明,將圖重畫于圖3.4.5b中。此時,電路處于直流工作狀態,也稱靜態,0點也稱為靜態工作點。當vs=ymsin ωt時(v<<yD),電路的負載線為
rd=-0.7v-0.5v/1ma=200
根據vθ的正負峰值+‰和-‰圖解可知,工作點將在o′和o″之間移動,則二極管電壓和電流變化為ΔvD和ΔjD。

直、交流電壓源同時作用時的二極管電路(a)電路圖 (b〉圖解分析
由上看出,在交流小信號vs的作用下,工作點沿v-r特性曲線,在靜態工作點o附近小范圍內變化,此時可把二極管v-f特性近似為以0點為切點的一條直線,其斜率的倒數就是小信號模型的微變電阻rd,由此得到小信號模型。


 公網安備44030402000607
公網安備44030402000607





