EC-B122 邏輯代數
發布時間:2019/10/9 19:52:19 訪問次數:994
EC-B122邏輯代數是1854年問世的,早年用于開關和繼電器網絡的分析、化簡,隨著半導體器件制造工藝的發展,各種具有良好開關性能的微電子器件不斷涌現,因而邏輯代數已成為分析和設計現代數字邏輯電路不可缺少的數學工具。
邏輯代數有一系列的定律、定理和規則,用它們對數學表達式進行處理,可以完成對邏輯電路的化簡、變換、分析和設計。
邏輯代數的基本定律和恒等式
根據第1章介紹過的邏輯與 、或 、非三 種基本運算法則可以推導出下面常用 的邏輯代數基本定律和恒等式 ,如表2.1.1所示 。

對表2.1.1所示定律和定理的證明方法是:列出等式左邊函數與右邊函數的真值表,如果等式兩邊的真值表相同,說明等式成立。
例如,要證明處+A=A時,令A=1,則A+A=1+1=1=A;再令A=0,
則A+A=0+0=0=A; 除此之外,別無其他可能,可見A+A=A。
在以上所有定律中,反演律具有特殊重要的意義。反演律又稱為摩根定理,它經常用于求一個原函數的非函數或者對邏輯函數進行變換。為了證明A+B=AB,AB=A+B,按A、B所有可能的取值情況列出真值表,如表2.1.2所示。將表中第3列和第4列進行比較、第5列和第6列進行比較,可見等式兩邊的真值表相同,故等式成立。
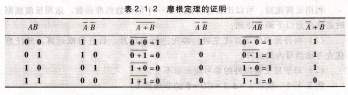
表2.1.1中的常用恒等式可以用其他基本定律加以證明 ,下面證明其中的第一條
AB+AC+BC=AB+AC+(A+A)BC
=AB+AC+ABC+ABC
=AB(1+C)+AC(1+B)
=AB+AC ・
這個恒等式說明,若兩個乘積項中分別包含因子A和A,而這兩個乘積項的其余因子組成第三個乘積項時,則第二個乘積項是多余的,可以消去。
本節所列出的基本公式反映了邏輯關系,而不是數量之間的關系,在運算中不能簡單套用初等代數的運算規則。例如初等代數中的移項規則就不能用,這是因為邏輯代數中沒有減法和除法的緣故。這一點在使用時必須注意。
系De M0gen的譯稱。
EC-B122邏輯代數是1854年問世的,早年用于開關和繼電器網絡的分析、化簡,隨著半導體器件制造工藝的發展,各種具有良好開關性能的微電子器件不斷涌現,因而邏輯代數已成為分析和設計現代數字邏輯電路不可缺少的數學工具。
邏輯代數有一系列的定律、定理和規則,用它們對數學表達式進行處理,可以完成對邏輯電路的化簡、變換、分析和設計。
邏輯代數的基本定律和恒等式
根據第1章介紹過的邏輯與 、或 、非三 種基本運算法則可以推導出下面常用 的邏輯代數基本定律和恒等式 ,如表2.1.1所示 。

對表2.1.1所示定律和定理的證明方法是:列出等式左邊函數與右邊函數的真值表,如果等式兩邊的真值表相同,說明等式成立。
例如,要證明處+A=A時,令A=1,則A+A=1+1=1=A;再令A=0,
則A+A=0+0=0=A; 除此之外,別無其他可能,可見A+A=A。
在以上所有定律中,反演律具有特殊重要的意義。反演律又稱為摩根定理,它經常用于求一個原函數的非函數或者對邏輯函數進行變換。為了證明A+B=AB,AB=A+B,按A、B所有可能的取值情況列出真值表,如表2.1.2所示。將表中第3列和第4列進行比較、第5列和第6列進行比較,可見等式兩邊的真值表相同,故等式成立。

表2.1.1中的常用恒等式可以用其他基本定律加以證明 ,下面證明其中的第一條
AB+AC+BC=AB+AC+(A+A)BC
=AB+AC+ABC+ABC
=AB(1+C)+AC(1+B)
=AB+AC ・
這個恒等式說明,若兩個乘積項中分別包含因子A和A,而這兩個乘積項的其余因子組成第三個乘積項時,則第二個乘積項是多余的,可以消去。
本節所列出的基本公式反映了邏輯關系,而不是數量之間的關系,在運算中不能簡單套用初等代數的運算規則。例如初等代數中的移項規則就不能用,這是因為邏輯代數中沒有減法和除法的緣故。這一點在使用時必須注意。
系De M0gen的譯稱。
上一篇:LTC2909ITS 數制
上一篇:IRU1010CSTR 代入規則



 公網安備44030402000607
公網安備44030402000607





