TK11128CSIL方波信號的時域
發布時間:2019/10/30 13:04:21 訪問次數:1766
TK11128CSIL對模擬電子電路進行測試。
由高等數學知識可知,任意周期函數只要滿足狄利克雷條件都可以展開成傅里葉級數。對于圖1.2.2的周期性方波信號,它的時間函數表達式為
v(t)=vs 當nt≤t<(2t+1)t/2時
v(t)=0 當(2n+1)t/2≤t((n+1)t時 (1.2.2)
式中vs為方波幅值,t為周期,n為從--∞到+∞的整數。

圖1.2.2和式(1.2.2)中的電壓v是時間t的函數,所以稱為方波信號的時域表達方式。
此方波信號可展開為傅里葉級數表達式
u(t)=vs/2+2vs/t(sinω0t+1/3sin3ωot+1/5sin5ωt+…) (⒈⒉3)
式中ωo=2t/t,vs/2是方波信號的直流分量,2vs/tsinω0t為該方波信號的基波,它
的周期釬與方波本身的周期相同。式(1.2.3)中其余各項都是高次諧波分量,它們的角頻率是基波角頻率的整數倍。根據三角函數知識,由式(1.2.3)可以得到如下形式:
v(t)=vs/2+2vs/t[cos(ω0t-t/2)+1/5cos(5ω0t-t/2)+...] (1.2.4)
即 V(t)=vs/2+2vs/t n=1,3,5... 1/ncos(nω0t-t/2) (1.2.5)
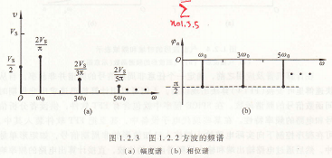
由此可以得到幅值與角頻率的關系為如圖1.2.3所示的圖解形式,其中包括直流項(ω=0)和每一諧波分量在相應角頻率處的振幅和相位。這種信號各頻率分量的振幅隨角頻率變化的分布,稱為該信號的幅度頻譜(簡稱幅度譜,如圖1.2.3a所示);而信號各頻率分量的相位隨角頻率變化的分布,稱為該信號的相位頻譜(簡稱相位譜,如圖1.2.3b所示),圖1.2.3稱為該方波信號的頻譜圖,是其頻域表達方式。對于正弦波,其頻譜只在基波頻率上有相應的幅值,其他頻率上的分量全部為零。
從傅里葉級數特性可知,許多周期信號的頻譜都由直流分量、基波分量以及無窮多項高次諧波分量所組成,頻譜表現為一系列離散頻率上的幅值,且隨著諧波次數的遞增,v(ω)的幅值總趨勢是逐漸減小的。如果只截取Ⅳω0(Ⅳ為有限正值)以下的信號組合,則可以得到原周期信號的近似波形,Ⅳ愈大,波形的誤差愈小。周期性方波信號亦可作為電子系統的測試信號,例如,當測試寬頻帶放大器的頻率響應時,固然可以采用掃頻儀來實現,但當采用方波信號進行測試時,由被測系統輸出方波電壓的前沿上升是否陡峭和平頂降落的程度,來定性地評價放大器的頻帶寬度。這是因為方波信號的前沿變化較快,反映高頻分量,而平頂部分變化較慢,反映低頻分量。詳見第4章4~8節。
上述正弦信號和方波信號都是周期信號,在一個周期內已包含了信號的全部信息,任何重復周期都沒有新的信息出現。客觀物理世界的信號遠沒有這么簡單,如果從時間函數來看,往往很難直螯弭一個簡單的表達式來描述,例如氣溫變化曲線可能如圖1.2.4a所示,它就是一非周期性時間函數波形。運用傅里葉變換可將非周期信號表達為一連續頻率函數形式的頻譜,它包含了所有可能的頻率(0≤ω<∞)成分。圖1.2,4b示意出圖a的頻譜函數。實際物理世界的各種非周期信號,隨角頻率上升到一定程度,其頻譜函數總趨勢是衰減的。當選擇適當的ωc(截止角頻率),把高于此頻率的部分截斷時,不致太多地影響信號的特性。通常把保留的部分稱為信號的帶寬。
由上分析可知,信號的頻域表達方式可以得到某些比時域表達方式更有意義的參數。信號的頻譜特性是電子系統有關頻率特性的主要設計依據。
TK11128CSIL對模擬電子電路進行測試。
由高等數學知識可知,任意周期函數只要滿足狄利克雷條件都可以展開成傅里葉級數。對于圖1.2.2的周期性方波信號,它的時間函數表達式為
v(t)=vs 當nt≤t<(2t+1)t/2時
v(t)=0 當(2n+1)t/2≤t((n+1)t時 (1.2.2)
式中vs為方波幅值,t為周期,n為從--∞到+∞的整數。

圖1.2.2和式(1.2.2)中的電壓v是時間t的函數,所以稱為方波信號的時域表達方式。
此方波信號可展開為傅里葉級數表達式
u(t)=vs/2+2vs/t(sinω0t+1/3sin3ωot+1/5sin5ωt+…) (⒈⒉3)
式中ωo=2t/t,vs/2是方波信號的直流分量,2vs/tsinω0t為該方波信號的基波,它
的周期釬與方波本身的周期相同。式(1.2.3)中其余各項都是高次諧波分量,它們的角頻率是基波角頻率的整數倍。根據三角函數知識,由式(1.2.3)可以得到如下形式:
v(t)=vs/2+2vs/t[cos(ω0t-t/2)+1/5cos(5ω0t-t/2)+...] (1.2.4)
即 V(t)=vs/2+2vs/t n=1,3,5... 1/ncos(nω0t-t/2) (1.2.5)
由此可以得到幅值與角頻率的關系為如圖1.2.3所示的圖解形式,其中包括直流項(ω=0)和每一諧波分量在相應角頻率處的振幅和相位。這種信號各頻率分量的振幅隨角頻率變化的分布,稱為該信號的幅度頻譜(簡稱幅度譜,如圖1.2.3a所示);而信號各頻率分量的相位隨角頻率變化的分布,稱為該信號的相位頻譜(簡稱相位譜,如圖1.2.3b所示),圖1.2.3稱為該方波信號的頻譜圖,是其頻域表達方式。對于正弦波,其頻譜只在基波頻率上有相應的幅值,其他頻率上的分量全部為零。
從傅里葉級數特性可知,許多周期信號的頻譜都由直流分量、基波分量以及無窮多項高次諧波分量所組成,頻譜表現為一系列離散頻率上的幅值,且隨著諧波次數的遞增,v(ω)的幅值總趨勢是逐漸減小的。如果只截取Ⅳω0(Ⅳ為有限正值)以下的信號組合,則可以得到原周期信號的近似波形,Ⅳ愈大,波形的誤差愈小。周期性方波信號亦可作為電子系統的測試信號,例如,當測試寬頻帶放大器的頻率響應時,固然可以采用掃頻儀來實現,但當采用方波信號進行測試時,由被測系統輸出方波電壓的前沿上升是否陡峭和平頂降落的程度,來定性地評價放大器的頻帶寬度。這是因為方波信號的前沿變化較快,反映高頻分量,而平頂部分變化較慢,反映低頻分量。詳見第4章4~8節。
上述正弦信號和方波信號都是周期信號,在一個周期內已包含了信號的全部信息,任何重復周期都沒有新的信息出現。客觀物理世界的信號遠沒有這么簡單,如果從時間函數來看,往往很難直螯弭一個簡單的表達式來描述,例如氣溫變化曲線可能如圖1.2.4a所示,它就是一非周期性時間函數波形。運用傅里葉變換可將非周期信號表達為一連續頻率函數形式的頻譜,它包含了所有可能的頻率(0≤ω<∞)成分。圖1.2,4b示意出圖a的頻譜函數。實際物理世界的各種非周期信號,隨角頻率上升到一定程度,其頻譜函數總趨勢是衰減的。當選擇適當的ωc(截止角頻率),把高于此頻率的部分截斷時,不致太多地影響信號的特性。通常把保留的部分稱為信號的帶寬。
由上分析可知,信號的頻域表達方式可以得到某些比時域表達方式更有意義的參數。信號的頻譜特性是電子系統有關頻率特性的主要設計依據。




 公網安備44030402000607
公網安備44030402000607





