W3A45A330KAT1A時間的函數
發布時間:2019/10/30 12:40:49 訪問次數:1071
W3A45A330KAT1A在人類的自然環境中,存在著各種各樣的信息。例如,眾所周知的氣候信息就包含溫度、氣壓、風速等信號。播音員播音時,微音器(話筒)將聲信號轉換為電信號,然后經過電子系統中的放大、濾波等電路,去驅動揚聲器,從而復制出播音員的聲音,為廣大聽眾所收聽。
由此可見,自然界的各種物理量必須首先經過傳感器將非電量轉換為電量,即電信號。這個信號是隨時間連續變化的,稱為模擬信號。處理模擬信號的各種電路,是本書所要討論的主要內容.
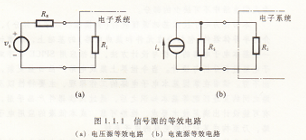
在處理各種信號時,需要對信號的表達與特性作簡要的介紹。將各種物理量轉換為可由電子電路處理的信號的傳感器,其輸出信號都是電信號。前述的微音器即是將聲音信號轉換為電信號的傳感器。為一般化起見,常把傳感器作為信號源看待。根據電路理論的知識可知,電路中的信號源都可以等效為如圖1.1,1所示的兩種形式。其中圖1.1.1a為以理想電壓源和源內阻R,并聯的等效信號源,稱為諾頓等效電路;這兩種信號源電路也可以等效輪換,可以根據不同的場合,使用不同的信號源形式.而圖1.1.1b以理想圖1.1,1 信號源的等效電路(a)電壓源等效電路 (b)電流源等效電路.
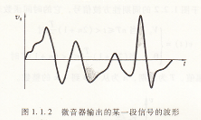
實際上信號都是與時間有關的,即是時間的函數。前述的微音器輸出的某一段信號的波形可能如圖1.1.2所示。這個波形看上去是無規則的,分析其特系Th6venin的譯稱。系Nonton的譯稱。等效信號源,秫為諾頓②等效電路亙這兩種信號源電路也可以等效轉以根據不同的場合,使用不同的信號源形式。
由于物理學的重大突破,電子技術在⒛世紀取得了驚人的進步。特別是近50年來,微電子技術和其他高技術的飛速發展,致使工業、農業、科技和國防等領域發生了令人矚目的變萆。與此同時,電子技術也正在改變著人們日常生活。收音機、電視機、高保真庋音響、DⅤD播放機、通信設各(程控電話機、移動通信機)、個人計算機等大量的電子產品,幾乎成為人們生活中不可缺少的部分。
本書作為電子技術基礎課程教材(含模擬和數字兩部分),在介紹半導體器件(包括分立元件和集成電路)的基礎上,著重討論一些基本電子電路的分析與設計方法,包括應用sPICE程序對電子電路進行分析與設計。當今世界上集成電路產品日益更新,層出不窮。讀者在掌握基本電子電路的工作原理、主要特性以及電路之間的互連匹配等基本知識之后,通過閱讀器件產品手冊,就有可能設計出滿足技術要求、性能可靠、成本低廉的應用電子電路,乃至構成某種功能完善的電子系統。
作為緒論,本章主要介紹電子電路的一些基本概念和放大電路的基本知識,為后續各章的學習提供引導性的背景知識。
性顯得有些困難,但已經有方法從中提取出它的特征參數。信號中的這些特征參數是設計放大電路和電子系統的重要依據。
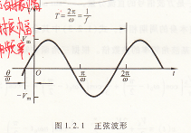
信號的頻譜,在信號分析中,為了簡化信號特征參數的提取,通常是將信號從時域變換到頻域.信號在頻域中表示的圖形或曲線稱為信號的頻譜.通過傅里葉變換可以實現信號從時域到頻域的變換.為了對信號的頻譜有進一步的了解,下面首先以正弦波電壓信號為例說明信號的表達方式及其基本特性.在此基礎上,以最典型的方波為例介紹頻譜的概念.圖1.2.1以最直觀的方式描述了正弦波電壓幅值與時間函數關系,其數學表達式為u(t)=vmsin(ωt+e) (1.2.1)
t=2t/ω=1/f
微音器輸出的某一段信號的波形丑懶求M壓幅值與時間的函數關系,其最典型的方波為例介紹頻譜的概念。圖1.2.1以最直觀的方式描述了正弦波電知信息,這是最簡單的信號。正因為如此,正弦波信號經常作為標準信號用來直流電壓信號.
W3A45A330KAT1A在人類的自然環境中,存在著各種各樣的信息。例如,眾所周知的氣候信息就包含溫度、氣壓、風速等信號。播音員播音時,微音器(話筒)將聲信號轉換為電信號,然后經過電子系統中的放大、濾波等電路,去驅動揚聲器,從而復制出播音員的聲音,為廣大聽眾所收聽。
由此可見,自然界的各種物理量必須首先經過傳感器將非電量轉換為電量,即電信號。這個信號是隨時間連續變化的,稱為模擬信號。處理模擬信號的各種電路,是本書所要討論的主要內容.
在處理各種信號時,需要對信號的表達與特性作簡要的介紹。將各種物理量轉換為可由電子電路處理的信號的傳感器,其輸出信號都是電信號。前述的微音器即是將聲音信號轉換為電信號的傳感器。為一般化起見,常把傳感器作為信號源看待。根據電路理論的知識可知,電路中的信號源都可以等效為如圖1.1,1所示的兩種形式。其中圖1.1.1a為以理想電壓源和源內阻R,并聯的等效信號源,稱為諾頓等效電路;這兩種信號源電路也可以等效輪換,可以根據不同的場合,使用不同的信號源形式.而圖1.1.1b以理想圖1.1,1 信號源的等效電路(a)電壓源等效電路 (b)電流源等效電路.
實際上信號都是與時間有關的,即是時間的函數。前述的微音器輸出的某一段信號的波形可能如圖1.1.2所示。這個波形看上去是無規則的,分析其特系Th6venin的譯稱。系Nonton的譯稱。等效信號源,秫為諾頓②等效電路亙這兩種信號源電路也可以等效轉以根據不同的場合,使用不同的信號源形式。

由于物理學的重大突破,電子技術在⒛世紀取得了驚人的進步。特別是近50年來,微電子技術和其他高技術的飛速發展,致使工業、農業、科技和國防等領域發生了令人矚目的變萆。與此同時,電子技術也正在改變著人們日常生活。收音機、電視機、高保真庋音響、DⅤD播放機、通信設各(程控電話機、移動通信機)、個人計算機等大量的電子產品,幾乎成為人們生活中不可缺少的部分。
本書作為電子技術基礎課程教材(含模擬和數字兩部分),在介紹半導體器件(包括分立元件和集成電路)的基礎上,著重討論一些基本電子電路的分析與設計方法,包括應用sPICE程序對電子電路進行分析與設計。當今世界上集成電路產品日益更新,層出不窮。讀者在掌握基本電子電路的工作原理、主要特性以及電路之間的互連匹配等基本知識之后,通過閱讀器件產品手冊,就有可能設計出滿足技術要求、性能可靠、成本低廉的應用電子電路,乃至構成某種功能完善的電子系統。
作為緒論,本章主要介紹電子電路的一些基本概念和放大電路的基本知識,為后續各章的學習提供引導性的背景知識。
性顯得有些困難,但已經有方法從中提取出它的特征參數。信號中的這些特征參數是設計放大電路和電子系統的重要依據。

信號的頻譜,在信號分析中,為了簡化信號特征參數的提取,通常是將信號從時域變換到頻域.信號在頻域中表示的圖形或曲線稱為信號的頻譜.通過傅里葉變換可以實現信號從時域到頻域的變換.為了對信號的頻譜有進一步的了解,下面首先以正弦波電壓信號為例說明信號的表達方式及其基本特性.在此基礎上,以最典型的方波為例介紹頻譜的概念.圖1.2.1以最直觀的方式描述了正弦波電壓幅值與時間函數關系,其數學表達式為u(t)=vmsin(ωt+e) (1.2.1)
t=2t/ω=1/f
微音器輸出的某一段信號的波形丑懶求M壓幅值與時間的函數關系,其最典型的方波為例介紹頻譜的概念。圖1.2.1以最直觀的方式描述了正弦波電知信息,這是最簡單的信號。正因為如此,正弦波信號經常作為標準信號用來直流電壓信號.




 公網安備44030402000607
公網安備44030402000607





