TMK063CH070FP-F電壓增益的模與角頻率
發布時間:2019/10/30 18:53:18 訪問次數:2052
TMK063CH070FP-F電壓增益=20lg au①dB (1.5.3)
電流增益=20lg ai dB (1.5.4)
由于功率與電壓(或電流)的平方成比例,因而功率增益表示為
功率增益=101gAPdB (1.5.5)
電壓增益Av和電流增益Ai之所以采用絕對值,是考慮到在某些情況下,av或Ai也許為負數,這意味著輸出與輸入之間的相位關系為180°,這與對數增益為負值時的意義是不同的,兩者不能混淆。例如,當放大電路的電壓增益為-20dB時,表示信號電壓經過放大電路后,衰減到原來的1/10,即|av|=0.1。
用對數方式表達放大電路的增益之所以在工程上得到廣泛的應用是由于:(1)當用對數坐標表達增益隨頻率變化的曲線時,可大大擴大增益變化的視野(見本書有關頻率響應的討論);(2)計算多級放大電路的總增益時,可將乘法化為加法進行運算。上述兩點有助于簡化電路的分析和設計過程。
頻率響應,在1.4節中所介紹的放大電路模型是極為簡單的模型,實際的放大電路中總是存在一些電抗性元件,如電容和電感元件以及電子器仵的極間電容、接線電容與接線電感等。因此,放大電路的輸出和輸人之間的關系必然和信號頻率有關。放大電路的頻率響應所指的是,在輸人正弦信號情況下,輸出隨輸人信號頻率連續變化的穩態響應。
若考慮電抗性元件的作用和信號角頻率變量,則放大電路的電壓增益可表達為
av(jω)=vo(jω)/vi(jω) (1,5.6)
av=Av(ω)∠rP(ω) (1.5.7)
或式中ω為信號的角頻率,av(ω)表示電壓增益的模與角頻率之間的關系,稱為幅頻響應;而♀(ω)表示放大電路輸出與輸人正弦電壓信號的相位差與角頻率之間的關系,稱為相頻響應,將二者綜合起來可全面表征放大電路的頻率響應。
圖1.5.4是一個普通音響系統放大電路的幅頻響應。為了符合通常習慣,橫坐標采用頻率單位r=ω/2π。值得注意的是,圖中的坐標均采用對數刻度,
電壓增益的表達棗是從功率的角度來考慮的,即10lgu02/ui2=20lguo/ui,此時設放大電路的輸人電阻Ri與輸出電阻Ro相等,實際上并非如此,只是利用這一概念而已。
放大電路的主要性能指標稱為波特圖①。這樣處理不僅把頻率和增益變化范圍展得很寬,而且在繪制近似頻率響應曲線時也十分簡便。詳見第4章4.7節。
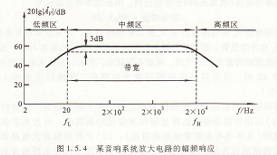
某音響系統放大電路的幅頻響應,所示幅頻響應的中間一段是平坦的,即增益保持常數ωdB,稱為中頻區(也稱為通帶區)。在⒛Hz和⒛kHz兩點增益分別下降3dB,而在低于⒛Hz和高于⒛kHz的兩個區域,增益隨頻率遠離這兩點而下降。在輸人信號幅值保持不變的條件下,增益下降3dB的頻率點,其輸出功率約等于
中頻區輸出功率的一半,通常稱為半功率點。一般把幅頻響應的高、低兩個半
功率點間的頻率差定義為放大電路的帶寬或通頻帶,即
Bw=fh-fl (1,5,8)
式中fh是頻率響應的高端半功率點,也稱為上限頻率,而尻則稱為下限頻率。由于通常有fl<<fh的關系,故有Bw≈fH。
有些放大電路的頻率響應,通頻帶一直延伸到直流,如圖1.5.5所示。可以認為它是圖1.5.4的一種特殊情況,即下限頻率為零。這種放大電路稱為直流(直接耦合)放大電路。現代模擬集成電路大多采用直接耦合的結構。
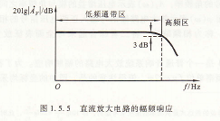
直流放大電路的幅頻響應,系Bode Pl∝的譯稱,由HW~Bodc所提出。
TMK063CH070FP-F電壓增益=20lg au①dB (1.5.3)
電流增益=20lg ai dB (1.5.4)
由于功率與電壓(或電流)的平方成比例,因而功率增益表示為
功率增益=101gAPdB (1.5.5)
電壓增益Av和電流增益Ai之所以采用絕對值,是考慮到在某些情況下,av或Ai也許為負數,這意味著輸出與輸入之間的相位關系為180°,這與對數增益為負值時的意義是不同的,兩者不能混淆。例如,當放大電路的電壓增益為-20dB時,表示信號電壓經過放大電路后,衰減到原來的1/10,即|av|=0.1。
用對數方式表達放大電路的增益之所以在工程上得到廣泛的應用是由于:(1)當用對數坐標表達增益隨頻率變化的曲線時,可大大擴大增益變化的視野(見本書有關頻率響應的討論);(2)計算多級放大電路的總增益時,可將乘法化為加法進行運算。上述兩點有助于簡化電路的分析和設計過程。
頻率響應,在1.4節中所介紹的放大電路模型是極為簡單的模型,實際的放大電路中總是存在一些電抗性元件,如電容和電感元件以及電子器仵的極間電容、接線電容與接線電感等。因此,放大電路的輸出和輸人之間的關系必然和信號頻率有關。放大電路的頻率響應所指的是,在輸人正弦信號情況下,輸出隨輸人信號頻率連續變化的穩態響應。
若考慮電抗性元件的作用和信號角頻率變量,則放大電路的電壓增益可表達為
av(jω)=vo(jω)/vi(jω) (1,5.6)
av=Av(ω)∠rP(ω) (1.5.7)
或式中ω為信號的角頻率,av(ω)表示電壓增益的模與角頻率之間的關系,稱為幅頻響應;而♀(ω)表示放大電路輸出與輸人正弦電壓信號的相位差與角頻率之間的關系,稱為相頻響應,將二者綜合起來可全面表征放大電路的頻率響應。
圖1.5.4是一個普通音響系統放大電路的幅頻響應。為了符合通常習慣,橫坐標采用頻率單位r=ω/2π。值得注意的是,圖中的坐標均采用對數刻度,
電壓增益的表達棗是從功率的角度來考慮的,即10lgu02/ui2=20lguo/ui,此時設放大電路的輸人電阻Ri與輸出電阻Ro相等,實際上并非如此,只是利用這一概念而已。
放大電路的主要性能指標稱為波特圖①。這樣處理不僅把頻率和增益變化范圍展得很寬,而且在繪制近似頻率響應曲線時也十分簡便。詳見第4章4.7節。

某音響系統放大電路的幅頻響應,所示幅頻響應的中間一段是平坦的,即增益保持常數ωdB,稱為中頻區(也稱為通帶區)。在⒛Hz和⒛kHz兩點增益分別下降3dB,而在低于⒛Hz和高于⒛kHz的兩個區域,增益隨頻率遠離這兩點而下降。在輸人信號幅值保持不變的條件下,增益下降3dB的頻率點,其輸出功率約等于
中頻區輸出功率的一半,通常稱為半功率點。一般把幅頻響應的高、低兩個半
功率點間的頻率差定義為放大電路的帶寬或通頻帶,即
Bw=fh-fl (1,5,8)
式中fh是頻率響應的高端半功率點,也稱為上限頻率,而尻則稱為下限頻率。由于通常有fl<<fh的關系,故有Bw≈fH。
有些放大電路的頻率響應,通頻帶一直延伸到直流,如圖1.5.5所示。可以認為它是圖1.5.4的一種特殊情況,即下限頻率為零。這種放大電路稱為直流(直接耦合)放大電路。現代模擬集成電路大多采用直接耦合的結構。

直流放大電路的幅頻響應,系Bode Pl∝的譯稱,由HW~Bodc所提出。



 公網安備44030402000607
公網安備44030402000607





