NCP1012APL130R曲線的切線方向
發布時間:2019/11/10 21:53:45 訪問次數:1836
NCP1012APL130R相對運動原理,作用在飛機上的空氣動力取決于飛機和空氣之間的相對運動情況,而與觀察、研究時所選用的參考坐標無關。也就是說,飛機以速度u在平靜的空氣中飛行時,作用在飛機上的空氣動力與遠方空氣以速度v流過靜止不動的飛機時所產生的空氣動力完全相同。這就是相對運動原理在空氣動力學中的應用。
空氣相對飛機的運動稱為相對氣流,相對氣流的方向與飛機運動的方向相反(見圖2-1)。只要相對氣流速度相同,產生的空氣動力也就相等。將飛機的飛行轉換為空氣的流動,使空氣動力問題的研究大大簡化。風洞實驗就是根據這個原理建立起來的。
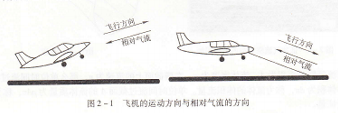
圖2-1 飛機的運動方向與相對氣流的方向
連續性假設是在進行空氣動力學研究時,將大量的、單個分子組成的大氣看成是連續的介質。所謂連續介質就是組成介質的物質連成一片,內部沒有任何空隙。在其中任意取一個微團都可以看成是由無數分子組成,微團表現出來的特性體現了眾多分子的共同特性。對大氣采用連續性假設的理由是與所研究的對象――飛機相比,空氣分子的平均自由行程要比飛機的尺寸小得多。空氣流過飛機表面時,與飛機之間產生的相互作用不是單個分子所為,而是無數分子共同作用的結果。
流場、定常流和非定常流,流體流動所占據的空間稱為流場。在流場中的任何一點處,如果流體微團流過時的流動參數――速度、壓力、溫度、密度等隨時間變化,這種流動就稱為非定常流,這種流場被稱為非定常流場。反之,如果流體微團流過時的流動參數――速度、壓力、溫度、密度等不隨時間變化,這種流動就稱為定常流,這種流場被稱為定常流場。
流線、流線譜、流管和流量,流線是在流場中用來描繪流體微團流動狀態的曲線。在流線每一點上,曲線的切線方向正是流體微團流過該點時流動速度的方向。在流場中,用流線組成的描繪流體微團流動情況的圖畫稱為流線譜。圖2-2所示為描繪氣流流過翼型的流線譜。如果流線譜不隨時間變化,它所描繪的就是定常流。
在流場中取一條不是流線的封閉曲線,通過曲線上各點的流線形成的管形曲面稱為流管,如圖2-3所示。因為通過曲線上各點流體微團的速度都與通過該點的流線相切,所以只有流管截面上有流體流過,而不會有流體通過管壁流進或流出。

圖2-2 低速氣流繞翼型的流動圖畫
若流管橫截面積為a,流體密度為ρ,在橫截面上的流速為v,那么單位時間流過截面a的流體體積為av,稱為流體的體積流量。單位時間流過截面姓的流體質量為pau,稱為流體的質量流量。
qm=pAv (2-1)
式中:gm――質量流量,單位kg/s。
流體流動的基本規律
連續方程是質量守恒定律在流體定常流動中的應用。圖2-4所示為遠方氣流以速度v繞流過機翼翼型的定常流線譜,選中一根流管和三個橫截面1、2、3。由式(2-1)可知:流體流過三個橫截面的質量流量分別等于qm1=ρlA1v1,qm2=p2a2u2,qm3=p3a3u3。流管性質決定了流管內的流體不能穿越管壁流到管外,流管外的流體也不能穿越管壁流到管內,根據質量守恒定律(質量不會自生也不會自滅),可以得出qm1=qm2=qm3.

圖2-4 繞翼型的流線譜
連續方程可以表述為:在定常流動中,流體連續并穩定的在流管中流動,通過流管各截面的質量流量相等。即:
ρ1a1u1=ρ2A2u2=ρ3a3u3=・・・ (2-2)
式中:ρ1、p2、p3…----流體流過各截面時的密度;
v1、u2、u3…----流體流過各截面時的速度;
a1、a2、a3…――流管各截面的面積。
對于不可壓縮流體,比如,低速飛行時(ma<0.4),可以把大氣看成是不可壓縮的流體,即密度ρ等于常數,連續方程可以簡化為:
A1v1=a2v2=A3v3=… (2-3)
這說明流體的流速與流管的橫截面積成反比:流管變細,流線變密,流速變快;流管變粗,流線變疏,流速變慢。
伯努利方程是能量守恒定律在流體流動中的應用。能量守恒定律是說在一個與外界隔絕的系統中,不論發生什么變化和過程,能量可以由一種形式轉變為另一種形式,但能量的總和保持恒定。對于不可壓縮的、理想的流體(沒有粘性)來說,在一個與外界沒有能量交換的系統中定常流動,流體具有的能量可以在壓力能和動能之間進行轉換,但能量的總和保持不變。伯努利方程只適用于不可壓縮的、理想的流體(沒有粘性)。因為對于不可壓縮的、理想的流體(沒有粘性)來說,流動中不會產生熱量,流體具有的能量形式只有壓力能、動能和重力勢能。流體在同一流管中流動,流管高度變化很小,可以認為流體的重力勢控制體Ω.
NCP1012APL130R相對運動原理,作用在飛機上的空氣動力取決于飛機和空氣之間的相對運動情況,而與觀察、研究時所選用的參考坐標無關。也就是說,飛機以速度u在平靜的空氣中飛行時,作用在飛機上的空氣動力與遠方空氣以速度v流過靜止不動的飛機時所產生的空氣動力完全相同。這就是相對運動原理在空氣動力學中的應用。
空氣相對飛機的運動稱為相對氣流,相對氣流的方向與飛機運動的方向相反(見圖2-1)。只要相對氣流速度相同,產生的空氣動力也就相等。將飛機的飛行轉換為空氣的流動,使空氣動力問題的研究大大簡化。風洞實驗就是根據這個原理建立起來的。

圖2-1 飛機的運動方向與相對氣流的方向
連續性假設是在進行空氣動力學研究時,將大量的、單個分子組成的大氣看成是連續的介質。所謂連續介質就是組成介質的物質連成一片,內部沒有任何空隙。在其中任意取一個微團都可以看成是由無數分子組成,微團表現出來的特性體現了眾多分子的共同特性。對大氣采用連續性假設的理由是與所研究的對象――飛機相比,空氣分子的平均自由行程要比飛機的尺寸小得多。空氣流過飛機表面時,與飛機之間產生的相互作用不是單個分子所為,而是無數分子共同作用的結果。
流場、定常流和非定常流,流體流動所占據的空間稱為流場。在流場中的任何一點處,如果流體微團流過時的流動參數――速度、壓力、溫度、密度等隨時間變化,這種流動就稱為非定常流,這種流場被稱為非定常流場。反之,如果流體微團流過時的流動參數――速度、壓力、溫度、密度等不隨時間變化,這種流動就稱為定常流,這種流場被稱為定常流場。
流線、流線譜、流管和流量,流線是在流場中用來描繪流體微團流動狀態的曲線。在流線每一點上,曲線的切線方向正是流體微團流過該點時流動速度的方向。在流場中,用流線組成的描繪流體微團流動情況的圖畫稱為流線譜。圖2-2所示為描繪氣流流過翼型的流線譜。如果流線譜不隨時間變化,它所描繪的就是定常流。
在流場中取一條不是流線的封閉曲線,通過曲線上各點的流線形成的管形曲面稱為流管,如圖2-3所示。因為通過曲線上各點流體微團的速度都與通過該點的流線相切,所以只有流管截面上有流體流過,而不會有流體通過管壁流進或流出。

圖2-2 低速氣流繞翼型的流動圖畫
若流管橫截面積為a,流體密度為ρ,在橫截面上的流速為v,那么單位時間流過截面a的流體體積為av,稱為流體的體積流量。單位時間流過截面姓的流體質量為pau,稱為流體的質量流量。
qm=pAv (2-1)
式中:gm――質量流量,單位kg/s。
流體流動的基本規律
連續方程是質量守恒定律在流體定常流動中的應用。圖2-4所示為遠方氣流以速度v繞流過機翼翼型的定常流線譜,選中一根流管和三個橫截面1、2、3。由式(2-1)可知:流體流過三個橫截面的質量流量分別等于qm1=ρlA1v1,qm2=p2a2u2,qm3=p3a3u3。流管性質決定了流管內的流體不能穿越管壁流到管外,流管外的流體也不能穿越管壁流到管內,根據質量守恒定律(質量不會自生也不會自滅),可以得出qm1=qm2=qm3.

圖2-4 繞翼型的流線譜
連續方程可以表述為:在定常流動中,流體連續并穩定的在流管中流動,通過流管各截面的質量流量相等。即:
ρ1a1u1=ρ2A2u2=ρ3a3u3=・・・ (2-2)
式中:ρ1、p2、p3…----流體流過各截面時的密度;
v1、u2、u3…----流體流過各截面時的速度;
a1、a2、a3…――流管各截面的面積。
對于不可壓縮流體,比如,低速飛行時(ma<0.4),可以把大氣看成是不可壓縮的流體,即密度ρ等于常數,連續方程可以簡化為:
A1v1=a2v2=A3v3=… (2-3)
這說明流體的流速與流管的橫截面積成反比:流管變細,流線變密,流速變快;流管變粗,流線變疏,流速變慢。
伯努利方程是能量守恒定律在流體流動中的應用。能量守恒定律是說在一個與外界隔絕的系統中,不論發生什么變化和過程,能量可以由一種形式轉變為另一種形式,但能量的總和保持恒定。對于不可壓縮的、理想的流體(沒有粘性)來說,在一個與外界沒有能量交換的系統中定常流動,流體具有的能量可以在壓力能和動能之間進行轉換,但能量的總和保持不變。伯努利方程只適用于不可壓縮的、理想的流體(沒有粘性)。因為對于不可壓縮的、理想的流體(沒有粘性)來說,流動中不會產生熱量,流體具有的能量形式只有壓力能、動能和重力勢能。流體在同一流管中流動,流管高度變化很小,可以認為流體的重力勢控制體Ω.



 公網安備44030402000607
公網安備44030402000607





