S-812C33AMC幅頻、相頻及穩定性有關數據
發布時間:2019/11/22 20:44:13 訪問次數:1790
S-812C33AMC表5-4所列為該系統在空載和負載狀態時的增益分貝數201gk、各轉折頻率(wj、wg、ωsp)、增益交接頻率ωc、相位延遲qc、相位裕度yg和幅值穩定裕度KG。

表5-4系統的幅頻、相頻及穩定性有關數據
由圖5-33、5-34及表5-4可得如下結論:
不加任何校正環節的該單臺發電機調壓系統,不論工作在空載狀態,還是額定狀
態,都是不穩定的,其穩定裕度γG和KG均為負值;
可通過降低系統的開環放大系數K,使幅頻特性向下移動,得到正值穩定裕度而
使系統穩定。然而,這樣勢必犧牲系統的靜態精度,即改善了動態穩定性,卻增加了靜態偏差;
既要使系統穩定,又要保證系統的靜態精度,需在系統中增設校正環節。校正環節的選擇,可根據系統的傳遞函數,以及所要求的系統性能,運用自動控制理論有關方法(如系統的零點、極點配置等)來確定。

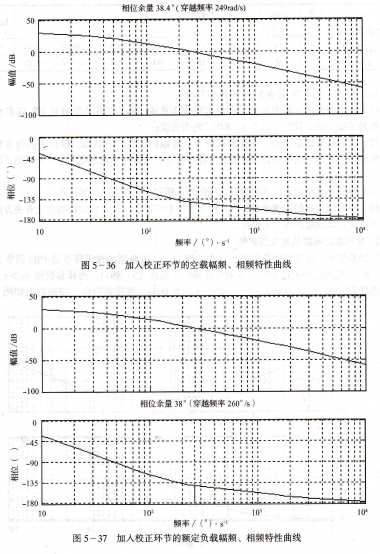
具有校正電路的系統穩定性,控制系統中,最常用的是串聯校正和并聯校正,最典型的校正環節是PID調節器(見圖5-30)。前面已分析過PID環節的傳遞函數(見式(5-88)),選擇參數使t2>r1>r3,這里選擇參數為r1=o.002s,t2=0.02s,r3=0.001s,其幅頻特性、相頻特性如圖5-35PID調節器幅頻特性、相頻特性所示。顯然,這是一個超前滯后網絡,它能補償系統的相位延遲,起到改善系統穩定性的作用。將校正環節加人系統,可以得到系統的開環幅相特性,如圖5-36、圖5-37所示。由于增設了校正電路,系統的穩定裕度為正。顯然,無論是空載還是負載此系統都是穩定的。
在介紹均衡線路之前,我們簡單回顧一下《電機學》中同步發電機的功角特性及并聯電源中的功率調節原理。
同步發電機的電磁功率和功角特性,同步發電機穩定運行時,原動機輸人機械功率P1,扣除電機的機械損耗、定子鐵耗p尼和附加損耗py后,余下的功率經電磁感應子PM,即有:
PM=P1-(pΩ十pFe+pf)
電磁功率扣除定子繞組的銅耗pcu后,就是向負載輸出的有功功率P2,即:
P2=PM-pcu (6-8)
一般銅耗很小,可略去不計,于是有:
PM≈P2=mUIcosq (6-9)
式中:m―同步發電機的相數;
U、i一發電機相電壓和負載相電流有效值;
cosq一負載功率因數。
以隱極電機為例,可推導出電磁功率的物理表達式:
pm=me0u/xssinq (6-10)
式中:E0一發電機的勵磁電勢,當勵磁電流不變時E0也為常數;
u―電網電壓,可認為是恒定值;
xs―隱極電機的同步電抗;
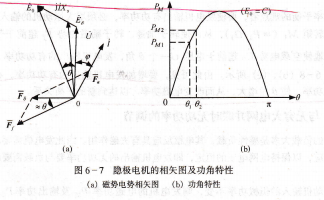
q---E0與u之間的相位差角。隱極電機的磁勢電勢相矢圖如圖6-7(a)所示。可見,當發電機的勵磁電流不變時,電磁功率大小只取決于ε角的大小,為功率角,PM=r(e)曲線稱為同步發電機的功角特性,如圖6-7(b)所示.
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
S-812C33AMC表5-4所列為該系統在空載和負載狀態時的增益分貝數201gk、各轉折頻率(wj、wg、ωsp)、增益交接頻率ωc、相位延遲qc、相位裕度yg和幅值穩定裕度KG。

表5-4系統的幅頻、相頻及穩定性有關數據
由圖5-33、5-34及表5-4可得如下結論:
不加任何校正環節的該單臺發電機調壓系統,不論工作在空載狀態,還是額定狀
態,都是不穩定的,其穩定裕度γG和KG均為負值;
可通過降低系統的開環放大系數K,使幅頻特性向下移動,得到正值穩定裕度而
使系統穩定。然而,這樣勢必犧牲系統的靜態精度,即改善了動態穩定性,卻增加了靜態偏差;
既要使系統穩定,又要保證系統的靜態精度,需在系統中增設校正環節。校正環節的選擇,可根據系統的傳遞函數,以及所要求的系統性能,運用自動控制理論有關方法(如系統的零點、極點配置等)來確定。

具有校正電路的系統穩定性,控制系統中,最常用的是串聯校正和并聯校正,最典型的校正環節是PID調節器(見圖5-30)。前面已分析過PID環節的傳遞函數(見式(5-88)),選擇參數使t2>r1>r3,這里選擇參數為r1=o.002s,t2=0.02s,r3=0.001s,其幅頻特性、相頻特性如圖5-35PID調節器幅頻特性、相頻特性所示。顯然,這是一個超前滯后網絡,它能補償系統的相位延遲,起到改善系統穩定性的作用。將校正環節加人系統,可以得到系統的開環幅相特性,如圖5-36、圖5-37所示。由于增設了校正電路,系統的穩定裕度為正。顯然,無論是空載還是負載此系統都是穩定的。

在介紹均衡線路之前,我們簡單回顧一下《電機學》中同步發電機的功角特性及并聯電源中的功率調節原理。
同步發電機的電磁功率和功角特性,同步發電機穩定運行時,原動機輸人機械功率P1,扣除電機的機械損耗、定子鐵耗p尼和附加損耗py后,余下的功率經電磁感應子PM,即有:
PM=P1-(pΩ十pFe+pf)
電磁功率扣除定子繞組的銅耗pcu后,就是向負載輸出的有功功率P2,即:
P2=PM-pcu (6-8)
一般銅耗很小,可略去不計,于是有:
PM≈P2=mUIcosq (6-9)
式中:m―同步發電機的相數;
U、i一發電機相電壓和負載相電流有效值;
cosq一負載功率因數。
以隱極電機為例,可推導出電磁功率的物理表達式:
pm=me0u/xssinq (6-10)
式中:E0一發電機的勵磁電勢,當勵磁電流不變時E0也為常數;
u―電網電壓,可認為是恒定值;
xs―隱極電機的同步電抗;
q---E0與u之間的相位差角。隱極電機的磁勢電勢相矢圖如圖6-7(a)所示。可見,當發電機的勵磁電流不變時,電磁功率大小只取決于ε角的大小,為功率角,PM=r(e)曲線稱為同步發電機的功角特性,如圖6-7(b)所示.

深圳市唯有度科技有限公司http://wydkj.51dzw.com/


 公網安備44030402000607
公網安備44030402000607





