VND3NV04 邏輯符號及其等效符號不是正負邏輯關系

發布時間:2020/2/9 21:45:32 訪問次數:2540

VND3NV04所以得到其等效符號,如圖3.5.2所示。

z=W・B

L=v+B

圖3.5.1 與非門及其等效符號

u=a+B

E=a・B

圖3.5.2 或非門及其等效符號

同理,利用摩根定律對與門和或門的邏輯表達式進行變換,可以得到它們的等效符號,分別如圖3.5.3和圖3.5.4所示。

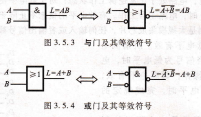
h=a+B=a/B

圖3.5.3 與門及其等效符號

圖3.5.4 或門及其等效符號

上述各圖所示的邏輯符號及其等效符號,是在同一邏輯體制下,用兩種不同的方式描述同一邏輯運算。因此,不能將等效符號看成是負邏輯體制或者負邏輯表示方法。本書采用正邏輯體制,所以對于輸人和輸出均是高電平為1,低電平為0。可以用真值表驗證各邏輯符號及其等效符號是等價的。

邏輯門等效符號的應用,利用邏輯門等效符號對邏輯電路進行變換,在不改變電路邏輯功能的前提下,可以簡化電路,以便能減少實現電路的門的種類或芯片的種類。

圖3.5.5(a)所示電路由兩級組成,第一級是兩個與門,第二級是一個或門。如果用標準集成芯片實現,需要與門和或門兩種芯片。

利用摩根定律X=X,在圖3.5.5(a)中間連線的兩端各加一個圓圈,相當于進行兩次非運算,但并沒有改變電路的功能,得到圖3.5.5(b)所示電路。然后將3.5.5(b)所示電路第二級的與非門的等效符號用與非門符號代替,就可以得到圖3.5.5(c)所示電路,該電路由三個與非門構成。一片74HC00包含4個2輸人與非門,因此,用一片即可實現圖3.5.5所示電路的邏輯功能。

參與運算符號,則在畫邏輯電路圖,或者驗證真值表時,應將其還原為低電平有效圖3.5.6中的G1門可以用包含六個非門的74HCT04實現。G2門是或門的等效符號,因此可以用包含4個2輸人的或門74HCT32實現。

需要注意的是,如果一根連線的兩端都有圓圈,并且都包含非運算的含義,可以用“圈圈相消”進行電路化簡,如圖3,5.5所示。但在圖3.5.6中,G2門的輸出與使能端之間的連線兩端也有圓圈,但這兩個圓圈不能抵消,因為集成芯片IC使能端的圓圈是表示低電平有效,不能去掉。

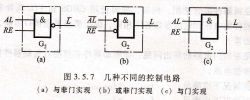
如果要求請求信號RE和允許信號Ab均為高電平有效,而芯片IC的使能端EⅣ仍為低有效,可以采用如圖3.5.7(a)所示的控制電路。G2門可以看成是輸人為高電平有效,輸出為低電平有效的與門,用一片包含4個2輸入的與非門74HCT00實現。

圖3.5.7 幾種不同的控制電路,(a)與非門實現 (b)或非門實現 (c)與門實現

如果要求請求信號RE和允許信號AI均為低電平有效,而芯片IC的使能端EⅣ為高電平有效,則采用如圖3.5.7(b)所示的控制電路。G2門可以看成是輸人為低電平有效,輸出為高電平有效的與門。根據圖3.5,2可知,G2門是或非門的等效符號,可以用或非門74HCT02實現。

同理,如果要求請求信號RE和允許信號AL均為高電平有效,芯片IC的使能信號也為高電平有效,則采用如圖3.5.7(c)所示的控制電路。G2門為輸人、輸出均是高電平有效的與門,用與門74HCT08實現。