浮點數的表示方法
發布時間:2014/6/1 21:44:11 訪問次數:1250
定點數表示方法簡單, QRD1114硬件實現成本也比較低,在低檔機型中得到了廣泛的應用。但是,由于小數點的位置是固定的,這使得定點數的數值表示范圍和表示精度相互矛盾,在使用過裎中受到較大限制。而在實際應用中,數值范圍很大的數其精度要求往往不高,而精度很高的數其數值范圍又往往很小。這就提醒我們,能否表示在有限位數的前提下,既可以表示絕對值很大的數(精度可以降低),也可以表示具有很高精度的數(數值范圍降低)。采用小數點位置浮動的方法,可以解決這個問題。
對任意一個二進制數Ⅳ來說,它總可以表示為一個純整數(或純小數)和一個2的整數次冪的乘積的形式:Ⅳ= 2P xS。其中S稱為Ⅳ的尾數;P稱為Ⅳ的階碼,可以決定小數點的位置;2稱為階碼的底。例如Ⅳ=1101.010101= 24×0.1101010101。為擴大數的表示范圍,在機器中都采用浮點數表示,此時階碼和尾數需要分別表示,并且有各自的符號位。
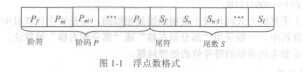
任何一個浮點數都由兩部分組成:階碼和尾數。階碼部分包括階符(Pf,1位)和階數(m位),是整數,尾數部分包括尾符(品1位)和尾數(聆位),是純小數,小數點隱藏在Sf和品之間。其中,Pf =0表示階碼為正,Pf=l表示階碼為負;Sf =0表示尾數為正數,Sf=1表示尾數為負數。雖然小數點隱藏在Sf和Sn之間,實際上Ⅳ的小數點位置是由階碼決定的。
同定點數相比,浮點數的優點是數的表示范圍很大,但缺點也較為明顯,其運算鞍為復雜,需要對階碼和尾數分別運算。
圖1.1描述的是一種原理性的浮點數格式,實際應用中的浮點數格式與其有一些差異。例如主流微機中流行的IEEE-754格式,其結構同圖1-1有較大差異。
定點數表示方法簡單, QRD1114硬件實現成本也比較低,在低檔機型中得到了廣泛的應用。但是,由于小數點的位置是固定的,這使得定點數的數值表示范圍和表示精度相互矛盾,在使用過裎中受到較大限制。而在實際應用中,數值范圍很大的數其精度要求往往不高,而精度很高的數其數值范圍又往往很小。這就提醒我們,能否表示在有限位數的前提下,既可以表示絕對值很大的數(精度可以降低),也可以表示具有很高精度的數(數值范圍降低)。采用小數點位置浮動的方法,可以解決這個問題。
對任意一個二進制數Ⅳ來說,它總可以表示為一個純整數(或純小數)和一個2的整數次冪的乘積的形式:Ⅳ= 2P xS。其中S稱為Ⅳ的尾數;P稱為Ⅳ的階碼,可以決定小數點的位置;2稱為階碼的底。例如Ⅳ=1101.010101= 24×0.1101010101。為擴大數的表示范圍,在機器中都采用浮點數表示,此時階碼和尾數需要分別表示,并且有各自的符號位。

任何一個浮點數都由兩部分組成:階碼和尾數。階碼部分包括階符(Pf,1位)和階數(m位),是整數,尾數部分包括尾符(品1位)和尾數(聆位),是純小數,小數點隱藏在Sf和品之間。其中,Pf =0表示階碼為正,Pf=l表示階碼為負;Sf =0表示尾數為正數,Sf=1表示尾數為負數。雖然小數點隱藏在Sf和Sn之間,實際上Ⅳ的小數點位置是由階碼決定的。
同定點數相比,浮點數的優點是數的表示范圍很大,但缺點也較為明顯,其運算鞍為復雜,需要對階碼和尾數分別運算。
圖1.1描述的是一種原理性的浮點數格式,實際應用中的浮點數格式與其有一些差異。例如主流微機中流行的IEEE-754格式,其結構同圖1-1有較大差異。


 公網安備44030402000607
公網安備44030402000607





