施密斯( Smith)預估控制算法
發布時間:2014/8/5 20:12:51 訪問次數:6747
1957年,施密斯( Smith)提出了一種純滯后的補償模型,但當時的模擬儀表無法實現,M5M51008CVP-55H直至后來利用計算機可以完成大滯后時間補償的預估控制。
如圖9 - 28歷示,G和下分別為控制對象的不包含滯后環節的傳遞函數和純滯后時間,該算法的核心是控制回路中增加Smith預估器G,(s)(1- e-TS),與常規控制器D(s)并聯共同組成純滯后補償控制器.
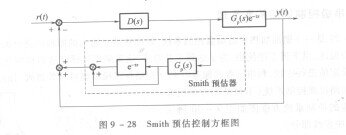
圖9 - 28 Smith預估控制方框圖
對常規控制器D(s)來說,包含原控制對象G,(s)e-T'與Smith預估器的廣義被控對象只相當于G,(s),即純滯后環節e…被放在了閉環控制回路之外。拉普拉斯變換的位移定理說明,e一僅將控制作用在時間坐標上推移了一個時間,控制系統的過渡過程及其他性能指標都與對象特性為G,(s)時完全相同。因此將Smith預估器與控制器并聯,理論上可以使控制對象的時間滯后得到完全補償。
采用模擬調節儀表實現上述Smith預估器比較困難,這是因為對象模型G,(s)各式各樣,純滯后環節由模擬電路e一模擬也很麻煩。相反地,由計算機來實現Smith預估器卻很容易。考慮到計算機控制系統中控制輸出后具有零階保持器,為了與離散化的被控對象對應,Smith預估器的離散化也采用零階保持器法,設Smith預估器的等效脈沖傳遞函數為GT (z).
一般地采樣周期r取純滯后時間r的整倍數關系。
上述Smith預估器G,(z)的輸入為控制器D(z)的輸出,式(9 -107)中后移算子:以通過計算機存儲單元的移位方便地實現。而數字控制器D(z)除了最常用的PID外,還可以是其他的控制算法。
一般認為,Smith預估補償方法是解決大滯后問題的有效方法,預估系統在模型基本準確時表現出良好的性能,但預估器對模型的精度或運行條件的變化十分敏感,對預估模型的精度要求較高,魯棒性較差。研究表明,簡單PID控制系統承受對象數變化的能力要強于帶有Smith預估器的系統。正是由于上述Smith預估器對模型誤差敏感的原因,限制了Smith預估補償方法在工業過程控制系統中的推廣應用。為了克服Smith預估器對模型誤差斂感、魯棒性差的不足,國內外控制界針對Smith預估器還提出了各種各樣的改進算法,這里就不一一介紹了。
1957年,施密斯( Smith)提出了一種純滯后的補償模型,但當時的模擬儀表無法實現,M5M51008CVP-55H直至后來利用計算機可以完成大滯后時間補償的預估控制。
如圖9 - 28歷示,G和下分別為控制對象的不包含滯后環節的傳遞函數和純滯后時間,該算法的核心是控制回路中增加Smith預估器G,(s)(1- e-TS),與常規控制器D(s)并聯共同組成純滯后補償控制器.

圖9 - 28 Smith預估控制方框圖
對常規控制器D(s)來說,包含原控制對象G,(s)e-T'與Smith預估器的廣義被控對象只相當于G,(s),即純滯后環節e…被放在了閉環控制回路之外。拉普拉斯變換的位移定理說明,e一僅將控制作用在時間坐標上推移了一個時間,控制系統的過渡過程及其他性能指標都與對象特性為G,(s)時完全相同。因此將Smith預估器與控制器并聯,理論上可以使控制對象的時間滯后得到完全補償。
采用模擬調節儀表實現上述Smith預估器比較困難,這是因為對象模型G,(s)各式各樣,純滯后環節由模擬電路e一模擬也很麻煩。相反地,由計算機來實現Smith預估器卻很容易。考慮到計算機控制系統中控制輸出后具有零階保持器,為了與離散化的被控對象對應,Smith預估器的離散化也采用零階保持器法,設Smith預估器的等效脈沖傳遞函數為GT (z).
一般地采樣周期r取純滯后時間r的整倍數關系。
上述Smith預估器G,(z)的輸入為控制器D(z)的輸出,式(9 -107)中后移算子:以通過計算機存儲單元的移位方便地實現。而數字控制器D(z)除了最常用的PID外,還可以是其他的控制算法。
一般認為,Smith預估補償方法是解決大滯后問題的有效方法,預估系統在模型基本準確時表現出良好的性能,但預估器對模型的精度或運行條件的變化十分敏感,對預估模型的精度要求較高,魯棒性較差。研究表明,簡單PID控制系統承受對象數變化的能力要強于帶有Smith預估器的系統。正是由于上述Smith預估器對模型誤差敏感的原因,限制了Smith預估補償方法在工業過程控制系統中的推廣應用。為了克服Smith預估器對模型誤差斂感、魯棒性差的不足,國內外控制界針對Smith預估器還提出了各種各樣的改進算法,這里就不一一介紹了。
上一篇:純滯后控制
上一篇:數字串級控制器的設計



 公網安備44030402000607
公網安備44030402000607





