1SMB5935BT3 邏輯仿真和邏輯綜合
發布時間:2019/10/10 17:36:47 訪問次數:1104
1SMB5935BT3邏輯代數是分析和設計邏輯電路的數學工具。一個邏輯問題可用邏輯函數來描述 ,邏輯函數可用真值表、邏輯表達式、卡諾圖和邏輯圖表達 ,這4種表達方式各具特點 ,可 根據需要選用。
HDL是一種以文本形式來描述數字系統硬件的結構和行為的語言 ,用它可以表示邏輯電路圖、邏輯表達式 ,還 可以表示更復雜的數字邏輯系統所完成的邏輯功能 (即行為 )。 計算機對HDL的處理包括兩個方面 :邏輯仿真和邏輯綜合。用 HDL設 計數字系統是當今的一種趨勢。
邏輯代數
用真值表證明下列恒等式:
(1) (A①B)C)C=a①(B①C)
(2) (A+B)(A+C)=a+BC
(3) a①B=aB+AB
寫出三變量的摩根定理表達式,并用真值表驗證其正確性。
用邏輯代數定律證明下列等式:
(1) A+AB=A+B
(2) ABC+aBC+AbC=AB+AC
(3) A+ABC+ACD+(C+D)E=a+CD+E
用代數法化簡下列各式:
(1) AB(BC+a (2) (A+B)(aB)
AB+ˉ1BC+△(召+△召)
(7) -B+ABC+△C+△B
(9) △BC D+△召I9+BC D+18C召£)+BC (10) △C+1”C+BC+A召C
將下列各式轉換成與一或形式:
(1)A①b①C①D
(2)A+B+C+D+C+D+△+D
(3) AC・BD BC・,1B
已知邏輯函數表達式為I=△BC D,ini出實現該式的邏輯電路圖,限使用非門
和二輸人與非門.
畫出實現下列邏輯表達式的邏輯電路圖,限使用非閘和二輸人與非閘。
(1) L=AB+AC
(2)I=D(A+C)
(3)l=(A+B)(C+D)
已知邏輯函數表達式為I=AB+AC,畫出實現該式的邏輯電路圖,限使用非門和二輸人或非門。
邏輯函數的卡諾圖化簡法
將下列函數展開為最小項表達式:
(1) l=ACD+BCD+aBCD
(2)l=A(B+C)
(3)l=aB+ABD(B+CD)
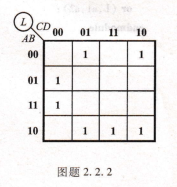
已知函數L(A,B,C,D)的卡諾圖如圖題2.2.2所不,試寫出函數L的最簡與或表達式。
用卡諾圖法化簡下列各式:
(1) ABCd+AbCI)+ab+AD+ABC
(2) (Ab+BD)C+BD(AC)+D(A+B)
00 01 11 10
00
(3) aBCI9+D(BCD) + (a+C) BD+,4(B+ri)
(4)L(a,B,C,D)=∑m(0,2,4,8△0,12) 01
(5)r(A,B,c,D)=∑m(0,1,2,5,6,8,9,10,13,14) 11
(6)E(A找C,D)=∑m(0,2,4,6,9,13)+∑“1, 10,3,5,7,11,15)
(7)I(a,B,C,D)=∑m(0,13,14,15)+∑d(1,2, 3,9,10,11)
1SMB5935BT3邏輯代數是分析和設計邏輯電路的數學工具。一個邏輯問題可用邏輯函數來描述 ,邏輯函數可用真值表、邏輯表達式、卡諾圖和邏輯圖表達 ,這4種表達方式各具特點 ,可 根據需要選用。
HDL是一種以文本形式來描述數字系統硬件的結構和行為的語言 ,用它可以表示邏輯電路圖、邏輯表達式 ,還 可以表示更復雜的數字邏輯系統所完成的邏輯功能 (即行為 )。 計算機對HDL的處理包括兩個方面 :邏輯仿真和邏輯綜合。用 HDL設 計數字系統是當今的一種趨勢。
邏輯代數
用真值表證明下列恒等式:
(1) (A①B)C)C=a①(B①C)
(2) (A+B)(A+C)=a+BC
(3) a①B=aB+AB
寫出三變量的摩根定理表達式,并用真值表驗證其正確性。
用邏輯代數定律證明下列等式:
(1) A+AB=A+B
(2) ABC+aBC+AbC=AB+AC
(3) A+ABC+ACD+(C+D)E=a+CD+E
用代數法化簡下列各式:
(1) AB(BC+a (2) (A+B)(aB)
AB+ˉ1BC+△(召+△召)
(7) -B+ABC+△C+△B
(9) △BC D+△召I9+BC D+18C召£)+BC (10) △C+1”C+BC+A召C
將下列各式轉換成與一或形式:
(1)A①b①C①D
(2)A+B+C+D+C+D+△+D
(3) AC・BD BC・,1B
已知邏輯函數表達式為I=△BC D,ini出實現該式的邏輯電路圖,限使用非門
和二輸人與非門.
畫出實現下列邏輯表達式的邏輯電路圖,限使用非閘和二輸人與非閘。
(1) L=AB+AC
(2)I=D(A+C)
(3)l=(A+B)(C+D)
已知邏輯函數表達式為I=AB+AC,畫出實現該式的邏輯電路圖,限使用非門和二輸人或非門。
邏輯函數的卡諾圖化簡法
將下列函數展開為最小項表達式:
(1) l=ACD+BCD+aBCD
(2)l=A(B+C)
(3)l=aB+ABD(B+CD)
已知函數L(A,B,C,D)的卡諾圖如圖題2.2.2所不,試寫出函數L的最簡與或表達式。
用卡諾圖法化簡下列各式:
(1) ABCd+AbCI)+ab+AD+ABC
(2) (Ab+BD)C+BD(AC)+D(A+B)
00 01 11 10
00
(3) aBCI9+D(BCD) + (a+C) BD+,4(B+ri)
(4)L(a,B,C,D)=∑m(0,2,4,8△0,12) 01
(5)r(A,B,c,D)=∑m(0,1,2,5,6,8,9,10,13,14) 11
(6)E(A找C,D)=∑m(0,2,4,6,9,13)+∑“1, 10,3,5,7,11,15)
(7)I(a,B,C,D)=∑m(0,13,14,15)+∑d(1,2, 3,9,10,11)




 公網安備44030402000607
公網安備44030402000607





