73800-2200 卡諾圖具有循環鄰接的特性
發布時間:2019/10/9 21:27:56 訪問次數:1268
73800-2200用卡諾圖化簡邏輯函數
化簡的依據,卡諾圖具有循環鄰接的特性,若圖中兩個相鄰的方格均為1,則這兩個相鄰最小項的和將消去一個變量。例如,圖2.2.6所示四變量卡諾圖中的方格5和方格7,其最小項之和為ABCD+ABCD=ABD(C+C)=ABD,消去了變量C,即消去了相鄰方格中不相同的那個因子。若卡諾圖中4個相鄰的方格為1,則這4個相鄰的最小項之和將消去2個變量,如上述四變量卡諾圖中的方格2、3、7、6,它們的最小項之和為
ABCD+ABCD+ABCD+ABCD=ABC(D+D)+ABC(D+D)
=ABC+ABC=AC
消去了變量B和D,即消去相鄰4個方格中不相同的那2個因子,這樣反復應用A+A=1的關系,就可使邏輯表達式得到簡化。這就是利用卡諾圖法化簡邏輯函數的基本原理。
化簡的步驟
用卡諾圖化簡邏輯函數的步驟如下:
將邏輯函數寫成最小項表達式。
按最小項表達式填卡諾圖,凡式中包含了的最小項,其對應方格填1,其余方格填0。
合并最小項。即將相鄰的1方格圈成一組(包圍圈),每一組含2n個方格,對應每個包圍圈寫成一個新的乘積項。本書中包圍圈用虛線框表示。
將所有包圍圈刈應的乘積項相加。
有時也可以由真值表直接填卡諾圖,以上的(1)、(2)兩步就合為一步。
畫包圍圈時應遵循以下原則:
包圍圈內的方格數必定是2N個,N等于0、1、2、3、…。
相鄰方格包括上下底相鄰,左右邊相鄰和四角相鄰。
同一方格可以被不同的包圍圈重復包圍,但新增包圍圈中一定要有新的方格 ,否則該包圍圈為多余。
包圍圈內的方格數要盡可能多 ,包圍圈的數目要盡可能少。 化簡后 ,一個包圍圈對應一個與項 (乘 積項 ) 圍圈越大 ,所得乘積項中的變量越少 。實際上 ,如 果做到了使每個包圍圈個數也就數也越多就最簡的與一或悉用卡諾圖化例2,2
L(A,B,C,D)
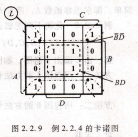
解 :由L畫出卡諾圖,如圖2.2.9 B.D所示 。
畫包圍圈合并最小項 ,得最簡與-或表達式L=BD+BD。
73800-2200用卡諾圖化簡邏輯函數
化簡的依據,卡諾圖具有循環鄰接的特性,若圖中兩個相鄰的方格均為1,則這兩個相鄰最小項的和將消去一個變量。例如,圖2.2.6所示四變量卡諾圖中的方格5和方格7,其最小項之和為ABCD+ABCD=ABD(C+C)=ABD,消去了變量C,即消去了相鄰方格中不相同的那個因子。若卡諾圖中4個相鄰的方格為1,則這4個相鄰的最小項之和將消去2個變量,如上述四變量卡諾圖中的方格2、3、7、6,它們的最小項之和為
ABCD+ABCD+ABCD+ABCD=ABC(D+D)+ABC(D+D)
=ABC+ABC=AC
消去了變量B和D,即消去相鄰4個方格中不相同的那2個因子,這樣反復應用A+A=1的關系,就可使邏輯表達式得到簡化。這就是利用卡諾圖法化簡邏輯函數的基本原理。
化簡的步驟
用卡諾圖化簡邏輯函數的步驟如下:
將邏輯函數寫成最小項表達式。
按最小項表達式填卡諾圖,凡式中包含了的最小項,其對應方格填1,其余方格填0。
合并最小項。即將相鄰的1方格圈成一組(包圍圈),每一組含2n個方格,對應每個包圍圈寫成一個新的乘積項。本書中包圍圈用虛線框表示。
將所有包圍圈刈應的乘積項相加。
有時也可以由真值表直接填卡諾圖,以上的(1)、(2)兩步就合為一步。
畫包圍圈時應遵循以下原則:
包圍圈內的方格數必定是2N個,N等于0、1、2、3、…。
相鄰方格包括上下底相鄰,左右邊相鄰和四角相鄰。
同一方格可以被不同的包圍圈重復包圍,但新增包圍圈中一定要有新的方格 ,否則該包圍圈為多余。
包圍圈內的方格數要盡可能多 ,包圍圈的數目要盡可能少。 化簡后 ,一個包圍圈對應一個與項 (乘 積項 ) 圍圈越大 ,所得乘積項中的變量越少 。實際上 ,如 果做到了使每個包圍圈個數也就數也越多就最簡的與一或悉用卡諾圖化例2,2
L(A,B,C,D)
解 :由L畫出卡諾圖,如圖2.2.9 B.D所示 。
畫包圍圈合并最小項 ,得最簡與-或表達式L=BD+BD。



 公網安備44030402000607
公網安備44030402000607





