98EX125-BCD自動并聯檢測電路
發布時間:2019/11/20 23:01:35 訪問次數:1164
98EX125-BCD式中:usm=2um/k一脈動電壓的最大值;
ωs=wg-ωc---角頻率之差;
△q=ωst一瞬時相位差。

圖6-20 變壓器原、副邊電壓波形
整流濾波后的電壓,變壓器副邊電壓△us經二極管D1半波整流,高頻部分被C1濾除,輸出的電壓可以近似地認為是振蕩電壓包絡線的正半部分。這是一個脈動電壓,其值可表示為:
Us=Usm/sin wst/2
=Usm sin △q/2 (6-30)
脈動電壓的波形如圖6-21所示。由圖可見, u、Us是一個周期性變化的脈動電壓,其脈動周期為:
Ts=1/fg-fc
=1/f
=2t/ws (6-31)
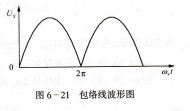
從式(6-31)可以看出,當頻差不同時,脈動電壓的周期也不同。頻差△F越小,脈
動周期Ts就越長。另外,從脈動電壓表達式可以看出,整流濾波后的脈動電壓(∫s的大小可以反映出瞬時相位差△田的大小。當△甲=ωsr=π時,Us=Us″z最大,相當于發電機電壓與電網電壓反相串聯,若此時合閘,則沖擊電流最大;當△甲=ωs莎=0或2π時,Us=0,說明此時發電機電壓與電網電壓同相位,這時合閘,則沖擊電流為零。所以應在LIs較小時合閘并聯。
通過以上分析可知,整流濾波后的脈動電壓us的大小可以反映出相位差的變化規律,而其周期的長短則反映出頻差的變化規律。
在以上的分析中,只考慮了電容C1對高頻部分的濾波,而沒有考慮C1充放電對Us的影響。正是由于C1充放電對Us的影響,決定了該電路只能在頻差△r和相差△甲較小時才能發出合閘信號。下面分析電容C1的展波作用。
電容器C1的展波作用,電容器C1兩端的電壓“c如圖6-22所示,取ωs莎在[-2π,0]內的情況來分析。在脈動電壓Us的作用下,電容C1或充電或放電,充電通道為B1-D1-C1,故充電時間常數很小;放電通道為C1一凡″,凡″為電阻R1、R2、u勤,
R3及三極管T1輸人電阻的串并聯等值電阻,然,放電時間常數了大于充電時間常數。
在[-2π,-π]區間內,Us給C1充電,由圖6-22 電容器充、放電波形于充電時間常數很小,故C1兩端電壓“c隨Us上升,即“c與Us一致。在[-π,一氣]區間內,L`s下降,C1通過電阻放電,Us下降速度小于電容放電速度,所以電容器仍被充電,“c與us仍一致。
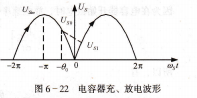
在[一氣,0]區間內,Us下降加快,“c按指數規律向電阻放電,直到嘰第二個周
期中的Us1值時,二極管D1又導通,I∶`s又向C1充電。如此反復,電容C1上的電壓波形如圖6-22所示。
下面推導電容器開始放電所對應的電角度(-ε0)的大小。
設電容器開始放電所對應的時間為一莎0,即有一ε0=-ω/0,則電容器開始放電的初始電壓Uc0為:
uc0=us0-ωst0=Us″sint
電容器按指數規律放電,其放電曲線為:
ri=∫usm sint)e^u
式中:T一電容器的放電時間常數。
當r=-u0時,電容器的放電速率為:
在[-π,0]內,脈動電壓的表達式為:
i=-Us″sint
當t=-h時,脈動電壓的下降率為:
ωoCt-n
=-Us-∞s-ui
因為在電容器開始放電時,放電速率與脈動電壓下降率相等,圖6-23 電容C1初始放電時刻隨△F的變化情況(a)△F大時 (b)△r小時
自動并聯檢測電路對頻差及相差的檢測
從圖6-23可以看出始放電電壓也較高,脈動電壓LJs的周期Ts較短,使得仍c還未下降到合閘電壓Jcz
所以,0為:ε0=2arctg(rπ△r) (6-40)
由上式可知,電容器C1的放電初始點與頻差△r及放電時間常數有關。如果放電時間常數r一定,ε0只與頻差△∫有關。如果頻差△F減小,則ε0減小,放電初始點曰將沿曲線下降,如圖6-23(a)、(b)所示。

98EX125-BCD式中:usm=2um/k一脈動電壓的最大值;
ωs=wg-ωc---角頻率之差;
△q=ωst一瞬時相位差。

圖6-20 變壓器原、副邊電壓波形
整流濾波后的電壓,變壓器副邊電壓△us經二極管D1半波整流,高頻部分被C1濾除,輸出的電壓可以近似地認為是振蕩電壓包絡線的正半部分。這是一個脈動電壓,其值可表示為:
Us=Usm/sin wst/2
=Usm sin △q/2 (6-30)
脈動電壓的波形如圖6-21所示。由圖可見, u、Us是一個周期性變化的脈動電壓,其脈動周期為:
Ts=1/fg-fc
=1/f
=2t/ws (6-31)

從式(6-31)可以看出,當頻差不同時,脈動電壓的周期也不同。頻差△F越小,脈
動周期Ts就越長。另外,從脈動電壓表達式可以看出,整流濾波后的脈動電壓(∫s的大小可以反映出瞬時相位差△田的大小。當△甲=ωsr=π時,Us=Us″z最大,相當于發電機電壓與電網電壓反相串聯,若此時合閘,則沖擊電流最大;當△甲=ωs莎=0或2π時,Us=0,說明此時發電機電壓與電網電壓同相位,這時合閘,則沖擊電流為零。所以應在LIs較小時合閘并聯。
通過以上分析可知,整流濾波后的脈動電壓us的大小可以反映出相位差的變化規律,而其周期的長短則反映出頻差的變化規律。
在以上的分析中,只考慮了電容C1對高頻部分的濾波,而沒有考慮C1充放電對Us的影響。正是由于C1充放電對Us的影響,決定了該電路只能在頻差△r和相差△甲較小時才能發出合閘信號。下面分析電容C1的展波作用。
電容器C1的展波作用,電容器C1兩端的電壓“c如圖6-22所示,取ωs莎在[-2π,0]內的情況來分析。在脈動電壓Us的作用下,電容C1或充電或放電,充電通道為B1-D1-C1,故充電時間常數很小;放電通道為C1一凡″,凡″為電阻R1、R2、u勤,
R3及三極管T1輸人電阻的串并聯等值電阻,然,放電時間常數了大于充電時間常數。
在[-2π,-π]區間內,Us給C1充電,由圖6-22 電容器充、放電波形于充電時間常數很小,故C1兩端電壓“c隨Us上升,即“c與Us一致。在[-π,一氣]區間內,L`s下降,C1通過電阻放電,Us下降速度小于電容放電速度,所以電容器仍被充電,“c與us仍一致。

在[一氣,0]區間內,Us下降加快,“c按指數規律向電阻放電,直到嘰第二個周
期中的Us1值時,二極管D1又導通,I∶`s又向C1充電。如此反復,電容C1上的電壓波形如圖6-22所示。
下面推導電容器開始放電所對應的電角度(-ε0)的大小。
設電容器開始放電所對應的時間為一莎0,即有一ε0=-ω/0,則電容器開始放電的初始電壓Uc0為:
uc0=us0-ωst0=Us″sint
電容器按指數規律放電,其放電曲線為:
ri=∫usm sint)e^u
式中:T一電容器的放電時間常數。
當r=-u0時,電容器的放電速率為:
在[-π,0]內,脈動電壓的表達式為:
i=-Us″sint
當t=-h時,脈動電壓的下降率為:
ωoCt-n
=-Us-∞s-ui
因為在電容器開始放電時,放電速率與脈動電壓下降率相等,圖6-23 電容C1初始放電時刻隨△F的變化情況(a)△F大時 (b)△r小時
自動并聯檢測電路對頻差及相差的檢測
從圖6-23可以看出始放電電壓也較高,脈動電壓LJs的周期Ts較短,使得仍c還未下降到合閘電壓Jcz
所以,0為:ε0=2arctg(rπ△r) (6-40)
由上式可知,電容器C1的放電初始點與頻差△r及放電時間常數有關。如果放電時間常數r一定,ε0只與頻差△∫有關。如果頻差△F減小,則ε0減小,放電初始點曰將沿曲線下降,如圖6-23(a)、(b)所示。



 公網安備44030402000607
公網安備44030402000607





