MC54HC194J 全定制或半定制的方法
發布時間:2020/2/8 18:19:01 訪問次數:904
MC54HC194J權碼的十進制數與二進制數之間可用下式來表示
(Ⅳ)D=T-363+W282+W131+WO30 (1.4.1)
式中50~60‰為二進制碼中各位的權。
余3碼是自補碼,與2421碼有類似的自補性。余3碼也是無權碼,它的每1位沒有一定的權值,不能用式(1.4.1)來表示其編碼關系,但其編碼可以由8421碼加3(0011)得出。
余3循環碼也是一種無權碼,它的特點是具有相鄰性,任意兩個相鄰代碼之間僅有1位取值不同,例如4和5兩個代碼0100和1100僅33不同。余3循環碼可以看成是將格雷碼首尾各3種狀態去掉而得到的。下面介紹格雷碼。
格雷系Gray的譯稱,格雷碼也是一種常見的無權碼,其編碼如表1.4.2所示。它也具有相鄰性,即兩個相鄰代碼之間僅有1位取值不同,因而常用于將模擬量轉換成用連續二進制數序列表示數字量的系統中。當模擬量發生微小變化而引起數字量從1位變化到相鄰位時,例如從3到4,格雷碼變化是從0010到0110,只有62位從0變成1,其余三位保持不變。如果對于自然二進制碼,其變化是從0011到0100,有3位發生變化,如果b2位從0到1變化所需的時間,比1和3。從1變到0的時間長,則在轉換過程中,會產生瞬間錯誤數碼0000出現。而格雷碼可以避免錯誤數碼的出現。
條件中只要有一個條件得到滿足,這件事就會發生。這種關系稱為或邏輯。或是指A閉合或B閉合,即任一個條件具各的意思。仿照前述,可以得出用0、1表示的或邏輯真值表,如表1,5.2所示。若用邏輯表達式來描述,則可寫為
L=A+B (1.5.2)
式中符號“+”表示A、B或運算,也稱為邏輯加。在某些文獻中,也有用符號V、∪來表示或運算,能實現或運算的邏輯電路稱為或門,其邏輯符號如圖1.5.2(b)和圖1.5.2(c)所示。圖1.5.2(b)所示為矩形符號,圖1.5.2(c)所示為特異形符號。
圖1.5.2 或邏輯運算狀態。若用邏輯表達式來描述,則rb>NC
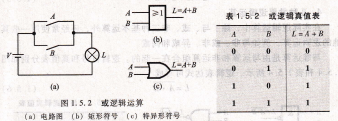
表1.5.2 或邏輯真值表
z=u+f
u=j+k
k的條件為依據。這種邏輯關系稱為非邏輯。若用0和1來表示繼電器和燈泡的狀態,A不通電和燈不亮用0表示,而A通電和燈亮用1表示,則得出非邏輯的真值表,如表1.5.3所示。

讀者很容易看到,b與A總是處于相反的邏輯可寫為
L=A (1.5.3)
表1.5.3 非邏輯真值表,二值邏輯變量與基本邏輯運算,(a)電路圖 (b)矩形符號 (c)特異形符號.
圖1.5.3 非邏輯運算,(a)電路圖 (b)矩形符號 (c)特異形符號
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
MC54HC194J權碼的十進制數與二進制數之間可用下式來表示
(Ⅳ)D=T-363+W282+W131+WO30 (1.4.1)
式中50~60‰為二進制碼中各位的權。
余3碼是自補碼,與2421碼有類似的自補性。余3碼也是無權碼,它的每1位沒有一定的權值,不能用式(1.4.1)來表示其編碼關系,但其編碼可以由8421碼加3(0011)得出。
余3循環碼也是一種無權碼,它的特點是具有相鄰性,任意兩個相鄰代碼之間僅有1位取值不同,例如4和5兩個代碼0100和1100僅33不同。余3循環碼可以看成是將格雷碼首尾各3種狀態去掉而得到的。下面介紹格雷碼。
格雷系Gray的譯稱,格雷碼也是一種常見的無權碼,其編碼如表1.4.2所示。它也具有相鄰性,即兩個相鄰代碼之間僅有1位取值不同,因而常用于將模擬量轉換成用連續二進制數序列表示數字量的系統中。當模擬量發生微小變化而引起數字量從1位變化到相鄰位時,例如從3到4,格雷碼變化是從0010到0110,只有62位從0變成1,其余三位保持不變。如果對于自然二進制碼,其變化是從0011到0100,有3位發生變化,如果b2位從0到1變化所需的時間,比1和3。從1變到0的時間長,則在轉換過程中,會產生瞬間錯誤數碼0000出現。而格雷碼可以避免錯誤數碼的出現。
條件中只要有一個條件得到滿足,這件事就會發生。這種關系稱為或邏輯。或是指A閉合或B閉合,即任一個條件具各的意思。仿照前述,可以得出用0、1表示的或邏輯真值表,如表1,5.2所示。若用邏輯表達式來描述,則可寫為
L=A+B (1.5.2)
式中符號“+”表示A、B或運算,也稱為邏輯加。在某些文獻中,也有用符號V、∪來表示或運算,能實現或運算的邏輯電路稱為或門,其邏輯符號如圖1.5.2(b)和圖1.5.2(c)所示。圖1.5.2(b)所示為矩形符號,圖1.5.2(c)所示為特異形符號。
圖1.5.2 或邏輯運算狀態。若用邏輯表達式來描述,則rb>NC

表1.5.2 或邏輯真值表
z=u+f
u=j+k
k的條件為依據。這種邏輯關系稱為非邏輯。若用0和1來表示繼電器和燈泡的狀態,A不通電和燈不亮用0表示,而A通電和燈亮用1表示,則得出非邏輯的真值表,如表1.5.3所示。

讀者很容易看到,b與A總是處于相反的邏輯可寫為
L=A (1.5.3)
表1.5.3 非邏輯真值表,二值邏輯變量與基本邏輯運算,(a)電路圖 (b)矩形符號 (c)特異形符號.
圖1.5.3 非邏輯運算,(a)電路圖 (b)矩形符號 (c)特異形符號
深圳市唯有度科技有限公司http://wydkj.51dzw.com/



 公網安備44030402000607
公網安備44030402000607





