T591 電路高通濾波特性的截止頻率
發布時間:2020/2/11 20:35:11 訪問次數:1983
R23=(2.235-1)R24≈24.7 kΩ

實際元件參數的誤差對傳遞函數的影響,請參閱9.3.3節例9.3,2的討論。
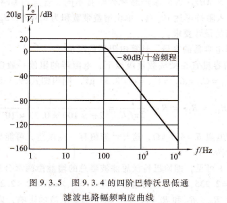
用SPICE仿真畫出波特圖,用SPICE仿真,可得到的幅頻響應波特圖如圖9,3.5所示(為了直觀,圖中橫坐標用r而不用ω表示)。由圖可見,201g40≈8.2dB。濾波器的截止頻率jk≈100 Hz,當F>gh時,曲線以80dB/十倍頻程衰減。因此,在F=10 kHz時,它從直流增益8.2dB下降了約160 dB。
201g|u|/du-40Hz=80Hz=120Hz
圖9.3.5 圖9.3.4的四階巴特沃思低通濾波,電路幅頻響應曲線.
用SPICE畫出各級和總的歸一化的幅頻響應曲線,四階巴特沃思低通濾波器各級歸一化幅頻響應曲線如圖9.3.6所示。前已十倍頻程信號處理與信號產生電路,R1同相比例,圖9.3.7 二階有源高通濾波電路

(A1+ut)c/ω=3u=2(9.3.12)1→0;而<ωc時,電路的特當ω傳遞,式(9.3.12)表明,當ω→∞,|A(u)|→A0;當ω→0,|A(jω)|=ωt時,|A(jω)|=a0/a2,ωc是3dB截止角頻率,因此在ω函數隨ω增加以幾×20 dB/十倍頻程上升c顯然,這是高通濾波|性。由式(9.3.12)可畫出巴特沃思高通濾波電路歸一化幅頻響應曲線,如圖9.3.8所示。由圖可見,隨著階數屁增加,其幅頻特性更接近理想特性。
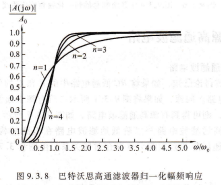
|/(jω)|0.6u=1
圖9.3.8 巴特沃思高通濾波器歸一化幅頻響應
例題作為一例,讓我們將圖9.3,4中的r1,R12,R13,R22和對應的C11.C12,C21,C22的位置互換,就可得到四階巴特沃思高通濾波電路(實際上也是兩個圖9.3.7所示的二階高通電路的級聯)c用SPICE仿真,可獲得其幅頻響應波特圖如圖9.3,9所示(為了直觀,圖中橫坐標同樣用r而不用ω表示)。由圖可見,該電路具有高通濾波特性,它的截止頻率五=100 Hzo在r(正時,隨F減42率信號處理與信號產生電路).
|A(jω)|=ω/ωc
R23=(2.235-1)R24≈24.7 kΩ

實際元件參數的誤差對傳遞函數的影響,請參閱9.3.3節例9.3,2的討論。
用SPICE仿真畫出波特圖,用SPICE仿真,可得到的幅頻響應波特圖如圖9,3.5所示(為了直觀,圖中橫坐標用r而不用ω表示)。由圖可見,201g40≈8.2dB。濾波器的截止頻率jk≈100 Hz,當F>gh時,曲線以80dB/十倍頻程衰減。因此,在F=10 kHz時,它從直流增益8.2dB下降了約160 dB。
201g|u|/du-40Hz=80Hz=120Hz
圖9.3.5 圖9.3.4的四階巴特沃思低通濾波,電路幅頻響應曲線.

用SPICE畫出各級和總的歸一化的幅頻響應曲線,四階巴特沃思低通濾波器各級歸一化幅頻響應曲線如圖9.3.6所示。前已十倍頻程信號處理與信號產生電路,R1同相比例,圖9.3.7 二階有源高通濾波電路

(A1+ut)c/ω=3u=2(9.3.12)1→0;而<ωc時,電路的特當ω傳遞,式(9.3.12)表明,當ω→∞,|A(u)|→A0;當ω→0,|A(jω)|=ωt時,|A(jω)|=a0/a2,ωc是3dB截止角頻率,因此在ω函數隨ω增加以幾×20 dB/十倍頻程上升c顯然,這是高通濾波|性。由式(9.3.12)可畫出巴特沃思高通濾波電路歸一化幅頻響應曲線,如圖9.3.8所示。由圖可見,隨著階數屁增加,其幅頻特性更接近理想特性。

|/(jω)|0.6u=1
圖9.3.8 巴特沃思高通濾波器歸一化幅頻響應
例題作為一例,讓我們將圖9.3,4中的r1,R12,R13,R22和對應的C11.C12,C21,C22的位置互換,就可得到四階巴特沃思高通濾波電路(實際上也是兩個圖9.3.7所示的二階高通電路的級聯)c用SPICE仿真,可獲得其幅頻響應波特圖如圖9.3,9所示(為了直觀,圖中橫坐標同樣用r而不用ω表示)。由圖可見,該電路具有高通濾波特性,它的截止頻率五=100 Hzo在r(正時,隨F減42率信號處理與信號產生電路).
|A(jω)|=ω/ωc



 公網安備44030402000607
公網安備44030402000607





