SP6656ER3-L 各門電路輸出的波形
發布時間:2020/2/8 17:39:12 訪問次數:1478
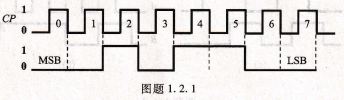
SP6656ER3-L數制一數字波形如圖題1.2.1所示,時鐘頻率為4 kHz,試確定:(1)它所表示的二進制數;(2)串行方式傳送8位數據所需要的時間;(3)以8位并行方式傳送數據時需要的時間。
1.2.2 將下列十進制數轉換為二進制數、八進制數和十六進制數(要求轉換誤差不大于2-4):
(1)43 (2)127 (3)254.25 (4)2,718
1.2.3 將下列二進制數轉換為十六進制數:
(1) (101001): (2) (11.01101):
1.2.4 將下列十進制數轉換為十六進制數(要求轉換誤差不大于16-4):
(1) (500)D (2) (59)D (3) (0.34)D (4) (1002,45)D
1.2.5 將下列十六制數轉換為二進制數:
(1) (23F.45)Ⅱ (2) (A040,51)Ⅱ
1.2.6 將下列十六進制數轉換為十進制數:
(1) (103,2)Ⅱ (2) (A45D.0BC)H
1.3 二進制數的算術運算
1.3.1 寫出下列二進制數的原碼、反碼和補碼:
(1) ( +1110): (2) ( +10110): (3) ( -1110): (4) ( -10110):
1.3.2 寫出下列有符號二進制補碼所表示的十進制數:
(1) 0010111 (2) 11101000
1.3.3 試用8位二進制補碼計算下列各式,并用十進制數表示結果:
(1) 12+9 (2) 11-3 (3) -29-25 (4) -120+30
1.4 二進制代碼
1.4.1 將下列十進制數轉換為8421BCD碼:
(1) 43 (2) 127 (3) 254.25 (4) 2.718
1.4.2 將下列數碼作為自然二進制數或8421BCD碼時,分別求出相應的十進制數:
(1)1(X)10111 (2)1⑾01(X)1(X)11 (3)(XX)101(X)1(X)1 (4)1(XXX)1(X).1(X)1(XX)1
1.4.3 試用十六進制數寫出下列字符的ASCII碼的表示:
(1) + (2)@ (3)you (4)43
1.6 邏輯函數及其表示方法
1.6.1 在圖題1.6.1中,已知輸入信號A、B的波形,畫出各門電路輸出z的波形。
則A+A=0+0=0=A; 除此之外,別無其他可能,可見A+c=A。
在以上所有定律中,反演律具有特殊重要的意義。反演律又稱為摩根定理,它經常用于求一個原函數的非函數或者對邏輯函數進行變換。為了證明A+B=AB,AB=A+B,按A、B所有可能的取值情況列出真值表,如表2.1.2所示。將表中第3列和第4列進行比較、第5列和第6列進行比較,可見等式兩邊的真值表相同,故等式成立。

表2.1.2 摩根定理的證明
AB+c
=AB(1+C)+AC(1+B)
=aB+AC
這個恒等式說明,若兩個乘積項中分別包含因子A和A,而這兩個乘積項的其余因子組成第三個乘積項時,則第二個乘積項是多余的,可以消去。
本節所列出的基本公式反映了邏輯關系,而不是數量之間的關系,在運算中不能簡單套用初等代數的運算規則。例如初等代數中的移項規則就不能用,這是因為邏輯代數中沒有減法和除法的緣故。這一點在使用時必須注意。
邏輯代數的基本規則,代入規則,在任何一個邏輯等式中,如果將等式兩邊出現的某變量Ab,都用一個函數代替,則等式依然成立,這個規則稱為代入規則。
例如,在B(A+C)=B4+BC中,將所有出現A的地方都用函數E+F代替,則等式仍成立,即得
aB[(E+F)+C]=B(E+F)+BC=BE+BF+BC
代人規則可以擴展所有基本定律或定理的應用范圍。例如前面用真值表證明了用二變量表示的摩根定理AB=A+B,若用L=CD代替等式中的A,則AB=A+B
表2.1.1中的常用恒等式可以用其他基本定律加以證明,下面證明其中的第一條邏輯代數.
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
SP6656ER3-L數制一數字波形如圖題1.2.1所示,時鐘頻率為4 kHz,試確定:(1)它所表示的二進制數;(2)串行方式傳送8位數據所需要的時間;(3)以8位并行方式傳送數據時需要的時間。

1.2.2 將下列十進制數轉換為二進制數、八進制數和十六進制數(要求轉換誤差不大于2-4):
(1)43 (2)127 (3)254.25 (4)2,718
1.2.3 將下列二進制數轉換為十六進制數:
(1) (101001): (2) (11.01101):
1.2.4 將下列十進制數轉換為十六進制數(要求轉換誤差不大于16-4):
(1) (500)D (2) (59)D (3) (0.34)D (4) (1002,45)D
1.2.5 將下列十六制數轉換為二進制數:
(1) (23F.45)Ⅱ (2) (A040,51)Ⅱ
1.2.6 將下列十六進制數轉換為十進制數:
(1) (103,2)Ⅱ (2) (A45D.0BC)H
1.3 二進制數的算術運算
1.3.1 寫出下列二進制數的原碼、反碼和補碼:
(1) ( +1110): (2) ( +10110): (3) ( -1110): (4) ( -10110):
1.3.2 寫出下列有符號二進制補碼所表示的十進制數:
(1) 0010111 (2) 11101000
1.3.3 試用8位二進制補碼計算下列各式,并用十進制數表示結果:
(1) 12+9 (2) 11-3 (3) -29-25 (4) -120+30
1.4 二進制代碼
1.4.1 將下列十進制數轉換為8421BCD碼:
(1) 43 (2) 127 (3) 254.25 (4) 2.718
1.4.2 將下列數碼作為自然二進制數或8421BCD碼時,分別求出相應的十進制數:
(1)1(X)10111 (2)1⑾01(X)1(X)11 (3)(XX)101(X)1(X)1 (4)1(XXX)1(X).1(X)1(XX)1
1.4.3 試用十六進制數寫出下列字符的ASCII碼的表示:
(1) + (2)@ (3)you (4)43
1.6 邏輯函數及其表示方法
1.6.1 在圖題1.6.1中,已知輸入信號A、B的波形,畫出各門電路輸出z的波形。
則A+A=0+0=0=A; 除此之外,別無其他可能,可見A+c=A。
在以上所有定律中,反演律具有特殊重要的意義。反演律又稱為摩根定理,它經常用于求一個原函數的非函數或者對邏輯函數進行變換。為了證明A+B=AB,AB=A+B,按A、B所有可能的取值情況列出真值表,如表2.1.2所示。將表中第3列和第4列進行比較、第5列和第6列進行比較,可見等式兩邊的真值表相同,故等式成立。

表2.1.2 摩根定理的證明
AB+c
=AB(1+C)+AC(1+B)
=aB+AC
這個恒等式說明,若兩個乘積項中分別包含因子A和A,而這兩個乘積項的其余因子組成第三個乘積項時,則第二個乘積項是多余的,可以消去。
本節所列出的基本公式反映了邏輯關系,而不是數量之間的關系,在運算中不能簡單套用初等代數的運算規則。例如初等代數中的移項規則就不能用,這是因為邏輯代數中沒有減法和除法的緣故。這一點在使用時必須注意。
邏輯代數的基本規則,代入規則,在任何一個邏輯等式中,如果將等式兩邊出現的某變量Ab,都用一個函數代替,則等式依然成立,這個規則稱為代入規則。
例如,在B(A+C)=B4+BC中,將所有出現A的地方都用函數E+F代替,則等式仍成立,即得
aB[(E+F)+C]=B(E+F)+BC=BE+BF+BC
代人規則可以擴展所有基本定律或定理的應用范圍。例如前面用真值表證明了用二變量表示的摩根定理AB=A+B,若用L=CD代替等式中的A,則AB=A+B
表2.1.1中的常用恒等式可以用其他基本定律加以證明,下面證明其中的第一條邏輯代數.
深圳市唯有度科技有限公司http://wydkj.51dzw.com/



 公網安備44030402000607
公網安備44030402000607





